 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XV турнир (февраль, 2000) >> Личная олимпиада >> 7 класс | Убрать решения |
|
|
| XV Уральский (VIII кировский) турнир юных математиков. Личная олимпиада. 7 класс |
|
|
(Р.Женодаров)
Решение: Можно. 532 делится на 14, а 215 делится на 43.Задача 2: Самолет вылетел из Москвы в час ночи 15 декабря по московскому времени и прибыл в город N в семь утра того же дня по местному времени. В полдень 15 декабря по N-скому времени он вылетел в город P и прибыл туда в 13.00 того же дня по P-скому времени. Через два часа он вылетел в Москву и вернулся туда в 18.00 15 декабря по московскому времени. Сколько времени самолет находился в воздухе? Ответ обязательно должен быть обоснован.
(И.Рубанов)
Решение: Самолет отсутствовал в Москве 17 часов с 1.00 до 18.00, при этом он находился на земле всего 7 часов – с 7.00 до 12.00 по местному времени в городе N и с 13.00 до 15.00 местного времени в городе P. Следовательно, все остальное время он летел.Задача 3: У Васи и Пети по 55 гирь весом 1, 2,, 55 кг. Они по очереди подкладывают свои гири – каждый на свою чашу двухчашечных весов. Первым ходит Вася. Петя выигрывает, если разность масс гирь на чашах окажется равной 50 кг. Сможет ли он этого добиться?
(Ю.Лифшиц)
Решение: Ответ. Да.1. Петя может просто повторять ходы Васи. В какой-то момент Вася вынужден будет сходить гирей 50 кг – и немедленно проиграет.
2. Петя откладывает в сторону свою 50-килограммовую гирю и ходит как угодно остальными гирями. В конце игры Вася выложит все гири, а Петя – все, кроме 50-килограммовой. Следовательно, чаша Васи будет весить на 50 кг тяжелее.
Задача 4: Пусть S(n) – сумма цифр числа n. Найдите все n, для которых
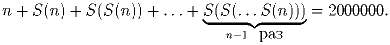
(О.Нечаева)
Решение: Ответ. Таких n не существует.Доказательство. Все n слагаемых в левой части дают одинаковый остаток при делении на 3, совпадающий с остатком от деления на 3 самого числа n. Перебирая три различных случая, получаем, что остаток от деления левой части на 3 равен либо 0, либо 1. Но правая часть – число 2000000 – при делении на 3 дает в остатке 2.
Задача 5: В треугольнике ABC ∠ A = 3 ∠ C. Точка D на стороне BC обладает тем свойством, что ∠ ADC = 2 ∠ C. Доказать, что AB + AD = BC.
(С.Берлов)
Решение: Продолжим отрезок BA за точку A и отложим на нем отрезок AE = AD. Заметим, что ∠ EAC = 180 – ∠ BAC = 180 – 3 ∠ C, поэтому треугольники ADC и AEC равны (по сторонам AC, AD = AE и углу между ними). Отсюда находим углы треугольника AEC: ∠ AEC = ∠ ADC = 2 ∠ C, ∠ ACE = ∠ C, т.е. ∠ BCE = 2 ∠ C, поэтому треугольник BEC равнобедренный. Таким образом, AB + AD = AB + AE = BE = BC.
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XV турнир (февраль, 2000) >> Личная олимпиада >> 7 класс | Убрать решения |