 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XV турнир (февраль, 2000) >> Турнир матбоёв >> Математический бой N1 >> Старшая группа, высшая лига | Показать решения |
|
|
| XV Уральский (VIII кировский) турнир юных математиков. Турнир матбоёв. Математический бой N1. Старшая группа, высшая лига |
|
|
(Американская олимпиада)
Задача 2: Через точку M – середину стороны AC треугольника ABC (AB ≠ BC) – провели прямую, параллельную биссектрисе угла B. Она пересекла прямую BC в точке X, а прямую AB – в точке Y. Через точки X и Y провели прямые, перпендикулярные BC и AB соответственно. Докажите, что точка их пересечения равноудалена от вершин A и C.
(С.Берлов)
Задача 3: Чертежный инструмент «треугольник" – это железный равносторонний треугольник со стороной 1. Можно приложить треугольник к любой точке или к любому ранее проведенному отрезку и обвести контур треугольника. Также разрешается соединять отрезком две точки на расстоянии не более 1. Докажите, что с помощью треугольника можно разделить данный отрезок пополам.
(Ю.Лифшиц)
Задача 4: На доске написано натуральное число. Первую цифру сложили со второй, вторую с третьей, и так далее, предпоследнюю цифру сложили с последней, после чего эти числа выписали в строчку без пробелов, сохраняя порядок. С полученным числом проделали такую же операцию, и так далее (например, из 1568 получается 61114, а из него, в свою очередь, 7225). Найдите наименьшее число, из которого такими операциями нельзя получить однозначное число.
(А.Переверзев)
Задача 5: Известно, что x > y > 0 и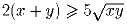 . Докажите,
что x ≥ 4y.
. Докажите,
что x ≥ 4y.
(А.Воронецкий)
Задача 6: Квадрат разбит на четное число прямоугольников. Докажите, что можно его разрезать на два многоугольника так, чтобы разрез шел по границам прямоугольников и в каждом многоугольнике оказалась половина всех прямоугольников.
(А.Шаповалов)
Задача 7: Чебурашка и Шапокляк поедают ящик апельсинов. За один ход Шапокляк может либо съесть один хороший апельсин, либо заменить два хороших апельсина на два гнилых, Чебурашка может либо съесть два хороших апельсина, либо съесть один хороший и выкинуть один гнилой. Первым ходит Чебурашка. Проигрывает тот, кто не сможет сделать ход. Кто выигрывает при правильной игре, если изначально в ящике было n хороших и ни одного гнилого апельсина?
(А.Храбров)
Задача 8: На острове Невезения 2000 жителей. Часть из них – лжецы, которые всегда лгут, а остальные – рыцари, которые всегда говорят правду. Каждый из них знает, кем – лжецом или рыцарем – является любой другой житель острова, кроме его ближайшего соседа (одного, если таких соседей несколько). Приехавший корреспондент перенумеровал всех жителей острова, а потом провел социологический опрос, и каждый опрошенный, имевший порядковый номер k, сказал: «Я знаю, что на острове не менее k лжецов". Докажите, что на острове есть два рыцаря, один из которых – ближайший сосед другого.(О.Нечаева, И.Рубанов)
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XV турнир (февраль, 2000) >> Турнир матбоёв >> Математический бой N1 >> Старшая группа, высшая лига | Показать решения |