 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XVII турнир (февраль, 2001) >> Командная олимпиада >> Старшая группа | Убрать решения |
|
|
| XVII Уральский (IX кировский) турнир юных математиков. Командная олимпиада. Старшая группа |
|
|
Имеются чашечные весы и четыре гири, сделанные из одинакового металла. Одна из них большая, другая поменьше, третья ещё меньше, а четвёртая – самая маленькая. Гири по очереди ставятся на чашки весов (на каждом шаге со стола берётся любая гиря и ставится на любую чашку весов). Известный хвастун Петя Сидоров не знает точного веса гирь, но заявляет, что сможет ставить гири на весы так, что сначала три раза перевесит левая чашка, а последний раз – правая. Стоит ли ему верить?
Решение: Упорядочим гири по убыванию веса: первая – самая тяжелая, гиря полегче – вторая, еще полегче – третья и самая маленькая, она же самая легкая – четвертая. Теперь положим на левую чашку вторую гирю. Левая чашка перевесит. Добавим к ней четвертую – без изменений. Поставим на правую чашку третью гирю. Левая чашка по-прежнему будет перевешивать, так как на ней есть вторая гиря – более тяжелая, чем третья. Теперь положим на правую чашку первую, самую тяжелую гирю. Правая чашка перевесит, так как первая гиря тяжелее второй, а третья тяжелее четвертой. Полный триумф Пети Сидорова! Задача 2:В трапеции ABCD с основанием AD AB = BC, AC = CD и BC + CD = AD. Найдите углы трапеции.
Решение:Отметим на основании AD трапеции точку K таким образом, что AK = BC. Тогда KD = CD и ABCK – ромб. Обозначим угол CAK через α . Получим, что ∠ CAK = ∠ ACK = ∠ ADC = α . Тогда ∠ CKD = ∠ KCD = 2 α , и из треугольника ACD находим, что 5 α = 180, откуда α = 36. Значит, углы трапеции таковы: ∠ A = 72, ∠ B = 108, ∠ C = 144, ∠ D = 36.
Задача 3:Сколькими способами из чисел 1, 2, … , 2n можно выбрать два или больше так, чтобы никакие два выбранных числа в сумме не давали 2n + 1?
Решение: 3n – 2n – 1. Разобьем все 2n чисел на пары чисел, дающих в сумме 2n + 1: (1,2n), (2,2n – 1), , (n,n + 1). Выбирая искомые числа, мы не можем брать два числа из одной пары. Поэтому из первой пары мы можем взять либо первое число 1, либо число 2n, либо не брать ничего. Те же три возможности для выбора мы имеем и для каждой из оставшихся n – 1 пар. Так как эти возможности независимы друг от друга, всего существует 3n наборов чисел, не содержащих двух чисел из одной пары. Среди них есть один пустой и 2n одноэлементных, а остальные 3n – 2n – 1 наборов нам подходят. Задача 4:Докажите, что для любых положительных чисел a, b, c, d и e выполнено неравенство
a² + b² + c² + d² + e² ≥ a(b + c + d + e)
Решение:0 ≤ (a/2 – b)² + (a/2 – c)² + (a/2 – d)² + (a/2 – e)² = a² – b – ac – ad – ae + b² + c² + d² + e², что и требовалось доказать.
Задача 5:В треугольнике ABC BC = 2AC, а D – такая точка на стороне BC, что ∠ DAC = ∠ ABC. Прямая AD пересекает биссектрису внешнего угла при вершине C в точке M. Докажите, что AM = AB.
Решение: Обозначим через N середину стороны BC. Тогда AC = CN = BN, ∠ ANB = 180° – ∠ ANC = 180° – (90° – ∠ ACN/2) = 90° + ∠ ACN/2 = ∠ ACM (поскольку ∠ ACM = ∠ ACN + ∠ MCN = ∠ ACN + (90° – ∠ ACN/2) = 90° + ∠ ACN/2). Тогда Δ ANB = Δ MCA (по стороне BN = CM и двум углам), откуда и следует, что AB = AM. Задача 6:p и q – нечетные простые числа. Сумма натуральных чисел a и b равна q, а ap + bp – точный квадрат. Докажите, что p = q.
Решение:Решение 1. Воспользуемся формулой
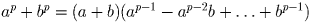 . По условию выражение в правой ее части равно
q(ap – 1 – ap – 2b + … + bp – 1).
Так как число ap + bp – точный квадрат, сумма в скобках должна
делиться на q. Рассмотрим выражение в скобках по модулю q.
По условию b ≡ – a (mod %)%q, а, значит,
. По условию выражение в правой ее части равно
q(ap – 1 – ap – 2b + … + bp – 1).
Так как число ap + bp – точный квадрат, сумма в скобках должна
делиться на q. Рассмотрим выражение в скобках по модулю q.
По условию b ≡ – a (mod %)%q, а, значит,
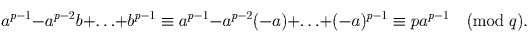
Число a меньше q, и, значит, не делится на q. Следовательно, на q должно делиться число p. Для простых p и q возможно только когда p = q, что и требовалось доказать.
Решение 2. Перепишем выражение из условия задачи, используя формулу бинома:
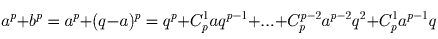
Все слагаемые в получившемся выражении и, следовательно, все выражение
делятся на q. Если это - точный квадрат, то оно делится и на q². Но
все слагаемые, кроме последнего, содержат множитель q², и,
следовательно,  тоже делится на
тоже делится на
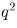 . Так как a не делится на q, должно быть p = q.
. Так как a не делится на q, должно быть p = q.
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XVII турнир (февраль, 2001) >> Командная олимпиада >> Старшая группа | Убрать решения |