 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XIV турнир (ноябрь, 1999) >> Математическая карусель >> Зачётные задачи. | Показать решения |
|
|
| XIV Уральский турнир юных математиков. Математическая карусель. Зачётные задачи. |
|
|
Сколькими способами можно разменять 1999 рублей 1-, 2- и 5- рублевыми монетами?
Задача 2:Сколько вершин может иметь выпуклый многоугольник, если известно, что число его диагоналей делится на число его вершин?
Задача 3:Какое слово зашифровано в числе 222122111121, если каждая буква заменена ее номером в русском алфавите?
Задача 4:Муха в полдень села на секундную стрелку часов и поехала, придерживаясь следующих правил: если она обгоняет какую-то стрелку или ее обгоняет какая-то стрелка (кроме секундной у часов есть часовая и минутная стрелки), то муха переползает на эту стрелку. Сколько кругов проедет муха в течение часа?
Задача 5:Из единичных кубиков составлен кубик размером 5х5х5. Какое наибольшее число кубиков можно из него удалить так, чтобы при взгляде на оставшуюся фигуру вдоль любого ребра был виден квадрат размером 5х5 без просветов? (Привести пример и объяснить, почему это наибольшее число.)
Задача 6:Вычислить 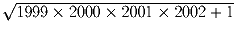 .
.
Какие натуральные числа нельзя представить в виде суммы двух взаимно простых чисел, больших 1?
Задача 8:В треугольнике ABC сторона AC – наибольшая. На ней (а не на ее продолжении) отложены отрезки AK = AB и CM = CB. Угол MBK равен 20. Найдите угол ABC.
Задача 9:Сколько существует трехзначных чисел, у которых сумма любых двух цифр делится на третью?
Задача 10:Сто туристов из ста городов (по одному из каждого города) путешествуют по этим городам. Каждые два из них знакомятся во время пребывания в городе, чужом для обоих. Турист Вася посетил городов не меньше, чем каждый из остальных. Какое наименьшее число чужих городов мог посетить Вася, если любые два туриста познакомились между собой? (Привести пример и объяснить, почему это наименьшее число).
Задача 11:Какое наибольшее число ненулевых цифр можно выбрать так, чтобы разность любых двух выбранных была невыбрана?
Задача 12:Доску 8 × 8 замостили 21 плиткой 1 × 3 без наложений. Сколько различных положений могла иметь непокрытая клетка?
Задача 13:Несколько (больше одного) шахматистов провели между собой матч-турнир в несколько кругов (в одном круге каждый с каждым сыграл по одной партии). Во сколько кругов прошло это соревнование, если всего было сыграно 224 партии?
Задача 14:На берегу реки отгорожено забором место с трех сторон в форме прямоугольника. Длина всего забора – 10 км. Какую наибольшую площадь может иметь этот участок?
Задача 15:Даны натуральные числа A и B. Известно, что из следующих четырех утверждений: а). A + 1 делится на B, б). A = 2B + 5, в). A + B делится на 3, г). A + 7B – простое число; три верных, а одно – неверное. Найти все возможные пары чисел A и B.
Задача 16:Вершины выпуклого многоугольника пронумерованы по порядку, начиная с 1, и число диагоналей, соединяющих вершины разной четности, в 2 раза больше числа диагоналей, соединяющих вершины с четными номерами. Сколько сторон могло быть у этого многоугольника?
Задача 17:В кружки буквы М впишите все цифры от 1 до 9 так, чтобы все суммы из трех чисел, стоящих по линиям буквы, были равными и наименьшими из возможных. (Приведите пример и укажите сумму)
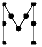
Найдите значения параметра x, при котором уравнения x³ + ax + 1 = 0 и x4 + ax² + 1 = 0 имеют общий корень.
Задача 19:Найдите угол A треугольника ABC, если он в три раза меньше угла BOC, где O – центр вписанной в треугольник окружности.
Задача 20:Найдите наименьшее значение функции 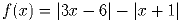 .
.
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XIV турнир (ноябрь, 1999) >> Математическая карусель >> Зачётные задачи. | Показать решения |