 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XV турнир (февраль, 2000) >> Турнир матбоёв >> Математический бой N4 >> Старшая группа, высшая лига | Показать решения |
|
|
| XV Уральский (VIII кировский) турнир юных математиков. Турнир матбоёв. Математический бой N4. Старшая группа, высшая лига |
|
|
(Польша, 1986)
Задача 2: Докажите, что существует натуральное число n такое, что в записи числа сразу после десятичной запятой подряд идут цифры 20001999.
(Украинская олимпиада, 1986)
Задача 3: В треугольнике ABC AB = BC. На стороне AB выбрана точка M, а на продолжении стороны AC – точка K такая, что KM = MC. Прямая, проходящая через точку B параллельно AC, пересекается с CM в точке P. Докажите, что прямая AP делит отрезок KM пополам.
(С.Берлов)
Задача 4: С написанными на доске положительными числами разрешается выполнить одну из двух следующих операций: 1) стереть произвольное число x и записать два раза число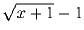 ;
2) стереть два
произвольных числа x и y и записать число x + y + xy. Изначально на доске
написано число a. Через несколько операций на доске оказалось
написано одно число. Докажите, что оно равно a.
;
2) стереть два
произвольных числа x и y и записать число x + y + xy. Изначально на доске
написано число a. Через несколько операций на доске оказалось
написано одно число. Докажите, что оно равно a.
(А.Проскурников)
Задача 5: Остап Бендер дает сеанс одновременной игры 45 шахматистам, сидящим по кругу. Напротив некоторых из шахматистов стоят стулья. Остап садится на стул перед шахматистом, и, сделав ход, переходит к следующему по часовой стрелке шахматисту. При этом он передвигает стул, если перед следующим шахматистом стула нет. Все стулья одинаковы. Могло ли случиться так, что в течение 2000 ходов Остапа ни разу не повторилось расположение стульев и Остапа (считается, что за это время ни одна из партий не закончится)? Задача 6: M – середина стороны AD выпуклого четырехугольника ABCD. Оказалось, что углы BAD, BMC и CDA равны 60. Докажите, что AB + CD = AM + BC.
(С.Берлов)
Задача 7: Во дворе стоят несколько столбов, некоторые пары соединены проводами. Всего протянуто mn проводов, и эти провода раскрашены в n цветов, причем ни от какого столба не отходят провода одинакового цвета. Докажите, что можно перекрасить эти провода так, чтобы проводов всех цветов было поровну и по-прежнему ни от какого столба не отходили два провода одного цвета.
(Украинская олимпиада, 1989)
Задача 8: Числа от 1 до 100 выписали в строку в некотором порядке. Среди любых трех подряд стоящих чисел подчеркнули среднее по величине. Какое наименьшее значение может принимать сумма всех подчеркнутых чисел?
(С.Берлов)
| Задачная база >> Соревнования всероссийского уровня >> Уральский турнир юных математиков >> XV турнир (февраль, 2000) >> Турнир матбоёв >> Математический бой N4 >> Старшая группа, высшая лига | Показать решения |