 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Зональный этап всероссийской олимпады. >> XXV >> 9 класс | Показать решения |
|
|
| Зональный этап XXV всероссийской математической олимпиады школьников, 1998/99 учебный год. 9 класс |
|
|
(Д.Кузнецов)
Задача 2: В треугольнике ABC на стороне AC нашлись такие точки D и E, что AB = AD и BE = EC (E между A и D). Точка F — середина дуги BC окружности, описанной около треугольника ABC. Докажите, что точки B, E, D, F лежат на одной окружности.(С.Берлов)
Задача 3: Произведение положительных чисел x, y и z равно 1.Известно, что 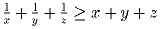 .
Докажите, что для любого натурального k выполнено неравенство
.
Докажите, что для любого натурального k выполнено неравенство
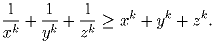
(С.Злобин)
Задача 4: Лабиринт представляет собой квадрат 8 × 8, в каждой клетке 1 × 1 которого нарисована одна из четырёх стрелок (вверх, вниз, вправо, влево). Верхняя сторона правой верхней клетки — выход из лабиринта. В левой нижней клетке находится фишка, которая каждым своим ходом перемещается на одну клетку в направлении, указанном стрелкой. После каждого хода стрелка в клетке, в которой только что была фишка, поворачивается на 90 по часовой стрелке. Если фишка должна сделать ходсквозь стенку квадрата, она остаётся на месте, но стрелка по-прежнему поворачивается на 90 по часовой стрелке. Докажите, что рано или поздно фишка выйдет из лабиринта.
(М. Антонов)
Задача 5:Все клетки клетчатой плоскости окрашены в 5 цветов так, что в любой фигуре вида 0,

все цвета различны. Докажите, что и в любой фигуре вида

все цвета различны.
(С.Берлов)
Задача 6:Задача 7:
Докажите, что каждое натуральное число является разностью двух натуральных чисел, имеющих одинаковое количество простых делителей. (Каждый простой делитель учитывается 1 раз, например, число 12 имеет два простых делителя: 2 и 3.)
(С.Токарев)
Задача 8:В треугольнике ABC (AB > BC) K и M — середины сторон AB и AC, O — точка пересечения биссектрис. Пусть P — точка пересечения прямых KM и CO, а точка Q такова, что QP ⊥ KM и QM||BO. Докажите, что QO ⊥ AC.
(М.Сонкин)
| Задачная база >> Соревнования всероссийского уровня >> Зональный этап всероссийской олимпады. >> XXV >> 9 класс | Показать решения |