 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Зональный этап всероссийской олимпады. >> XXV >> 9 класс | Убрать решения |
|
|
| Зональный этап XXV всероссийской математической олимпиады школьников, 1998/99 учебный год. 9 класс |
|
|
(Д.Кузнецов)
Решение:Ответ: 29. Поскольку однозначные числа не имеют общих цифр, то N > 9. А так как числа, соседние с числом 9, должны содержать девятку в своей записи, то меньшее из них не может быть меньше, чем 19, а большее — меньше, чем 29. Следовательно, N ≥ 29.
Равенство N = 29 возможно, поскольку условиям задачи удовлетворяет, например, такой порядок расстановки чисел от 1 до 29 по кругу: 1, 11, 10, 20, 21, 12, 2, 22, 23, 3, 13, 14, 4, 24, 25, 5, 15, 16, 6, 26, 27, 7, 17, 18, 8, 28, 29, 9, 19.
Задача 2: В треугольнике ABC на стороне AC нашлись такие точки D и E, что AB = AD и BE = EC (E между A и D). Точка F — середина дуги BC окружности, описанной около треугольника ABC. Докажите, что точки B, E, D, F лежат на одной окружности.(С.Берлов)
Решение:Обозначим ∠ BDA через 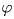 . Тогда
. Тогда
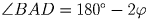 , (AB = AD),
, (AB = AD),
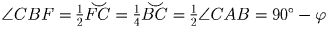 . Точки E и F равноудалены
от точек B и C, поэтому FE — серединный перпендикуляр к отрезку
BC, следовательно,
. Точки E и F равноудалены
от точек B и C, поэтому FE — серединный перпендикуляр к отрезку
BC, следовательно, 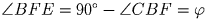 .
Итак,
.
Итак, 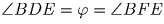 , т.е. точки B, F, D, E
— на одной окружности.
, т.е. точки B, F, D, E
— на одной окружности.
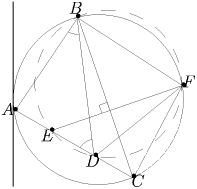
Известно, что 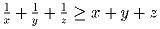 .
Докажите, что для любого натурального k выполнено неравенство
.
Докажите, что для любого натурального k выполнено неравенство
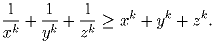
(С.Злобин)
Решение:Если abc = 1, то неравенства
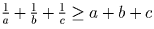 и
(a – 1)(b – 1)(c – 1) ≤ 0 равносильны.
Действительно, из того, что
и
(a – 1)(b – 1)(c – 1) ≤ 0 равносильны.
Действительно, из того, что 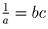 ,
, 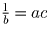 ,
,
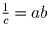 и abc – 1 = 0 следует, что они оба равносильны неравенству
bc + ca + ab ≥ a + b + c.
Кроме того, числа t – 1 и tk – 1 имеют при k > 0
одинаковый знак.
Поэтому
и abc – 1 = 0 следует, что они оба равносильны неравенству
bc + ca + ab ≥ a + b + c.
Кроме того, числа t – 1 и tk – 1 имеют при k > 0
одинаковый знак.
Поэтому
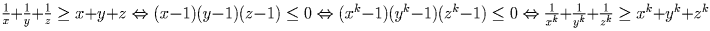 .
.
Задача 4: Лабиринт представляет собой квадрат 8 × 8, в каждой клетке 1 × 1 которого нарисована одна из четырёх стрелок (вверх, вниз, вправо, влево). Верхняя сторона правой верхней клетки — выход из лабиринта. В левой нижней клетке находится фишка, которая каждым своим ходом перемещается на одну клетку в направлении, указанном стрелкой. После каждого хода стрелка в клетке, в которой только что была фишка, поворачивается на 90 по часовой стрелке. Если фишка должна сделать ход
сквозь стенку квадрата, она остаётся на месте, но стрелка по-прежнему поворачивается на 90 по часовой стрелке. Докажите, что рано или поздно фишка выйдет из лабиринта.
(М. Антонов)
Решение:Предположим, что фишка никогда не выйдет из лабиринта. Тогда на клетку с номером 1 фишка попадёт конечное число раз (менее 4), т.к. в противном случае, когда стрелка покажет на выход, фишка из лабиринта уйдёт. Аналогично получаем, что после того, как фишка в последний раз побывает на поле <<1>>, она конечное число раз побывает на полях с номером <<2>>. Продолжая рассуждения получаем, что на поле с номером k, 1 ≤ k ≤ 14 она конечное число раз побывает на поле с номером k + 1. Значит, на каждом поле фишка побывает конечное число раз, что противоречит неограниченности числа ходов. Следовательно, фишка должна выйти из лабиринта.
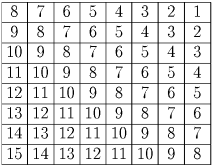
Задача 5:
Все клетки клетчатой плоскости окрашены в 5 цветов так, что в любой фигуре вида 0,

все цвета различны. Докажите, что и в любой фигуре вида

все цвета различны.
(С.Берлов)
Решение:Предположим, что в некоторой фигуре 1 × 5 отсутствует некоторый цвет, например, синий (на рисунке эта фигура выделена). Тогда в каждой паре клеток, обозначенных одинаковыми буквами, присутствует синий цвет (в противном случае его не будет в одной из крестообразных фигур, включающих эти пары клеток). Но тогда одна из двух крестообразных фигур, включающих клетки, обозначенные буквами a и c, содержит 2 клетки синего цвета. Противоречие.
Задача 6:
Задача 7:
Докажите, что каждое натуральное число является разностью двух натуральных чисел, имеющих одинаковое количество простых делителей. (Каждый простой делитель учитывается 1 раз, например, число 12 имеет два простых делителя: 2 и 3.)
(С.Токарев)
Решение:Если данное число n — чётно, т.е. n = 2m, то искомыми числами будут k = 4m и l = 2m.
Пусть n — нечётно, p1, … ,ps — его простые делители и p — наименьшее нечетное простое число, не входящее во множество p1, … ,ps. Тогда искомыми будут числа k = pn и l = (p – 1)n, так как, в силу выбора p, число p – 1 имеет своими делителями число 2, и, возможно, какие-то из чисел p1, … ,ps.
Задача 8:
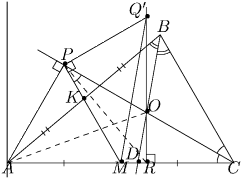
В треугольнике ABC (AB > BC) K и M — середины сторон AB и AC, O — точка пересечения биссектрис. Пусть P — точка пересечения прямых KM и CO, а точка Q такова, что QP ⊥ KM и QM||BO. Докажите, что QO ⊥ AC.
(М.Сонкин)
Решение: Опустим перпендикуляр OR на прямую AC. Пусть перпендикуляр к прямой KM, восставленный в точке P, пересекает прямую OR в точке Q′. Достаточно доказать, что MQ′||BO, т.к. это будет означать, что точки Q и Q′ совпадают. Так как KM||BC, то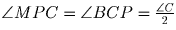 .
Тогда в
.
Тогда в 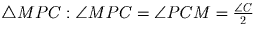 , откуда
MP = MC = MA, поэтому точка P лежит на окружности с диаметром AC и
∠ APC = 90.
, откуда
MP = MC = MA, поэтому точка P лежит на окружности с диаметром AC и
∠ APC = 90.В четырёхугольнике APOR ∠ APO = ∠ ARO = 90, следовательно
он вписанный, отсюда 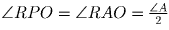 ( ∠ RPO = ∠ RAO опираются на одну дугу).
( ∠ RPO = ∠ RAO опираются на одну дугу).
В четырёхугольнике MPQ′R ∠ MPQ′ = ∠ MRQ′ = 90,
следовательно, он вписанный, отсюда
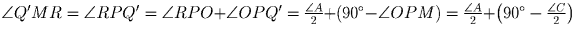 .
Если BO пересекает AC в точке D, то
из ∆ BCD:
.
Если BO пересекает AC в точке D, то
из ∆ BCD: 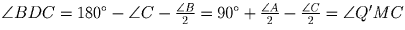 .
Отсюда MQ′||BO.
.
Отсюда MQ′||BO.
| Задачная база >> Соревнования всероссийского уровня >> Зональный этап всероссийской олимпады. >> XXV >> 9 класс | Убрать решения |