 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Зональный этап всероссийской олимпады. >> XXVII >> 8 класс | Убрать решения |
|
|
| Зональный этап XXVII всероссийской математической олимпиады школьников, 2000/2001 учебный год. 8 класс |
|
|
(Р.Женодаров)
Решение: Ответ: Нельзя. Пусть число l получается из числа n изменением на k процентов (n, l — натуральные, k — целое). Тогда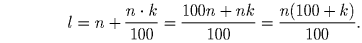
Аналогично, 9 может быть только последним. Но на последнем месте может быть только одно число, поэтому требуемая расстановка невозможна.
Задача 2: N цифр — единицы и двойки — расположены по кругу. Изображенным назовем число, образуемое несколькими цифрами, расположенными подряд (по часовой стрелке или против часовой стрелки). При каком наименьшем значении N все четырехзначные числа, запись которых не содержит цифр, отличных от 1 и 2, могут оказаться среди изображенных?
(С.Волчёнков)
Решение: Ответ: 14. Заметим, что изображения чисел 1111, 2112 и 2122 не могут иметь общих единиц, а изображения чисел 2222, 1221 и 1211 — общих двоек. Следовательно, если все эти числа встречаются среди изображенных, то по кругу должны располагаться не менее 14 цифр — 7 единиц и 7 двоек.Равенство N = 14 возможно, и соответствующий пример расположения цифр показан на рис.
iv01.82
Задача 3: Все стороны выпуклого пятиугольника равны, а все углы различны. Докажите, что максимальный и минимальный углы прилегают к одной стороне пятиугольника.
(Д.Джукич)
Решение: Предположим противное. Рассмотрим пятиугольник ABCDE, удовлетворяющий условиям задачи. Не умаляя общности, можно считать, что угол A — наибольший, а угол D — наименьший (любую пару несмежных вершин можно перевести в эту переобозначениями).Заметим, что ∠ EAC = ∠ A – ∠ BAC = ∠ A – ∠ ACB > ∠ C – ∠ BCA = ∠ ACD.
Предположим, что лучи AE и CD пересекаются в точке X. Тогда в треугольнике ACX сторона CX больше стороны AX, так как против нее лежит больший угол. Тогда DX = CX – CD = CX – AE > AX – AE = EX, поэтому 180 – ∠ E > 180 – ∠ D, что противоречит минимальности угла D.
Случаи, когда прямые AE и CD параллельны или пересекаются с другой стороны от ED, аналогичны.
iv01.83
Задача 4: Уголком размера n × m, где m,n ≥ 2, называется фигура, получаемая из прямоугольника размера n × m клеток удалением прямоугольника размера (n – 1) × (m – 1) клеток.Два игрока по очереди делают ходы, заключающиеся в закрашивании в уголке произвольного ненулевого количества клеток, образующих прямоугольник или квадрат. Пропускать ход или красить одну клетку дважды нельзя. Проигрывает тот, после чьего хода все клетки уголка окажутся окрашенными. Кто из игроков победит при правильной игре?
(Д.Храмцов)
Решение: Ответ: Независимо от соотношения n и m победит первый игрок.Укажем выигрышную стратегию для первого игрока. Можно считать, что m ≤ n. Если m = 2, то первый своим ходом красит всю б'ольшую сторону уголка, оставляя второму одну клетку и выигрывает. Далее считаем n ≥ m ≥ 3. В этом случае первый красит на большей стороне n – m + 1 клетку, начиная с угловой, после чего остается две одинаковых полоски по m – 1 клетке. Далее первый игрок симметрично повторяет в другой полоске ходы второго, сделанные в одной из полосок до тех пор, пока после хода второго не останется единственного незакрашенного прямоугольника из более чем одной клетки. Затем, если число незакрашенных одноклеточных прямоугольников к этому моменту нечетно, то первый красит неодноклеточный прямоугольник целиком, а если четно, то оставляем в нем одну незакрашенную клетку. Таким образом, после его хода останется нечетное количество некрашенных прямоугольников, каждый из которых одноклеточный, поэтому последний ход вынужден будет сделать второй игрок, в результате чего и проиграет.
Задача 5: Пусть a, b, c, d, e и f — некоторые числа, причем a • c • e ≠ 0. Известно, что значения выражений |ax + b| + |cx + d| и |ex + f| равны при всех значениях x. Докажите, что ad = bc.
(Р.Женодаров)
Решение: Пусть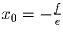 . Тогда
. Тогда
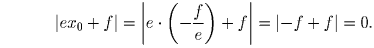
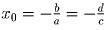 , поэтому
, поэтому
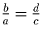 или ad = bc.
Задача 6:
Натуральное число n назовем хорошим, если каждое из чисел n,
n + 1, n + 2 и n + 3 делится на сумму своих цифр.
(Например, n = 60398 — хорошее.) Обязательно ли предпоследней
цифрой хорошего числа, оканчивающегося восьмеркой, будет девятка?
или ad = bc.
Задача 6:
Натуральное число n назовем хорошим, если каждое из чисел n,
n + 1, n + 2 и n + 3 делится на сумму своих цифр.
(Например, n = 60398 — хорошее.) Обязательно ли предпоследней
цифрой хорошего числа, оканчивающегося восьмеркой, будет девятка?
(В.Замков)
Решение: Ответ: Обязательно. Допустим, что нашлось хорошее число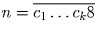 ,
где c1, … ,ck — цифры, причем ck ≠ 9.
Тогда
,
где c1, … ,ck — цифры, причем ck ≠ 9.
Тогда 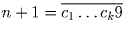 ,
, 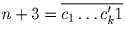 ,
где c′k = ck + 1.
,
где c′k = ck + 1.Числа n + 1 и n + 3 нечетны, а суммы их цифр равны c1 + c2 + … + ck + 9 и c1 + c2 + … + ck + 2 соответственно. Эти суммы отличаются на 7, и потому одна из них четна. Но четное число не может быть делителем нечетного. Противоречие.
Задача 7: Можно ли клетки доски 5 × 5 покрасить в 4 цвета так, чтобы клетки, стоящие на пересечении любых двух строк и любых двух столбцов, были покрашены не менее чем в 3 цвета?
(О.Подлипский)
Решение: Ответ: Нет. Предположим, что существует раскраска таблицы 5 × 5, удовлетворяющая условию. Рассмотрим эту таблицу (см. рис.). По принципу Дирихле в каждом столбце найдется цвет, в который покрашены по крайней мере две клетки этого столбца. Назовем такой цвет преобладающим для данного столбца (возможно у какого-то столбца будет два преобладающих цвета). Аналогично, какой то цвет (назовем его <<1>>) будет преобладающим для двух столбцов. Поскольку от перестановки строк и столбцов ничего не зависит, будем считать, что это столбцы a и b. Также можем считать, что в первом столбце цветом 1 покрашены клетки a4 и a5. Тогда клетки b4 и b5 должны быть покрашены какими-то двумя различными цветами, отличными от цвета 1. Пусть они покрашены цветами 2 и 3, а поскольку цвет 1 — преобладающий для столбца b, можем считать, что клетки b2 и b3 покрашены цветом 1. Рассмотрим клетку a3. Выбрав 3 и 4 строку и столбцы a и b, мы получим, что клетка a3 не может быть покрашенной цветами 1 и 3. Выбрав 3 и 5 строку и столбцы a и b, мы получим, что клетка a3 не может быть покрашенной цветами 1 и 2. То есть клетка a3 покрашена цветом 4. Но из аналогичных рассуждений мы получаем, что и клетка a2 покрашена цветом 4. То есть квадрат, состоящий из клеток a3, a2, b3 и b2 покрашен в два цвета — противоречие.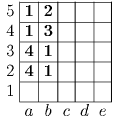
(Л.Емельянов)
Решение: Пусть AC — б'ольшая сторона ∆ ABC, A1C1 — средняя линия, параллельная AC, а M — середина A1C1. Так как ∠ A и ∠ C — острые, то M проектируется внутрь отрезка AC, пусть B1 — эта проекция (см. рис.).Проведем 2 разреза B1C1 и B1A1. Так как B1M — медиана и высота ∆ A1B1C1, то C1B1 = A1B1. Q — симметрична B1 относительно A1, P — симметрична B1 относительно C1.
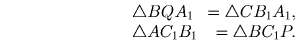
iv01.881iv01.882
| Задачная база >> Соревнования всероссийского уровня >> Зональный этап всероссийской олимпады. >> XXVII >> 8 класс | Убрать решения |