 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Зональный этап всероссийской олимпады. >> XXVII >> 9 класс | Убрать решения |
|
|
| Зональный этап XXVII всероссийской математической олимпиады школьников, 2000/2001 учебный год. 9 класс |
|
|
(Н.Агаханов)
Решение: Ответ: Верно.Решение 1. Вначале Коля будет изменять коэффициент b до тех пор, пока b не попадет в промежуток [ – 2,0]. Петя ходами в 1 не сможет помешать ему сделать это.
Теперь если 1) b = 0, то Коля выиграл (трехчлен f = x² + ax имеет целые корни); 2) b = – 1, то Петя, чтобы не проиграть, должен получить b = – 2, так как если он оставит b = – 1, то следующим ходом Коля сделает b = 0.
Итак, получен коэффициент b = – 2 и Петя не может изменять его, так как коэффициент b = – 1 или b = – 3 Коля своим ходом сразу превратит в 0.
Далее Коля будет изменять на 3 коэффициент a до тех пор, пока тот не попадет в промежуток – 1,1.
Если a = ± 1, то он выиграл: трехчлен f = x² ± x – 2 имеет целые корни. Если же a = 0, то следующим ходом уже Петя получит такой трехчлен.
Решение 2. Покажем, что Коля всегда может получить трехчлен, один из корней которого равен 2. Тогда из теоремы Виета (x1 + x2 = – a) будет следовать, что и второй корень — целый. Для этого ему нужно добиться равенства: f(2) = 4 + 2a + b = 0, т.е. 2a + b = – 4. Но Петя может изменять выражение A = 2a + b на ± 2 (изменив a), либо на ± 1, изменив b, а Коля — на ± 2, ± 6, ± 1, ± 3. Изменяя b на ± 3, Коля может получить A ∈ [ – 3, – 5]. Из A = – 3 Петя получит A = – 5, – 1 , – 4 (проигрыш), – 2 и следующим ходом Коля получит A = – 4.
Из A = – 5 Петя получит A = – 3, – 7, – 4 (проигрыш), – 6 и Коля получает A = – 4.
Задача 3: В параллелограмме ABCD на сторонах AB и BC выбраны точки M и N соответственно так, что AM = NC, Q — точка пересечения отрезков AN и CM. Докажите, что DQ — биссектриса угла D.
(Л.Емельянов)
Решение: Пусть P — точка пересечения прямых AN и DC (см. рис.). Тогда утверждение задачи равносильно следующему равенству: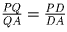 . Пусть AB = CD = a, AD = BC = b, AM = CN = c
и CD = x. Тогда из подобия треугольников NCP и ADP следует
. Пусть AB = CD = a, AD = BC = b, AM = CN = c
и CD = x. Тогда из подобия треугольников NCP и ADP следует
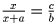 , откуда
, откуда 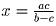 и
и 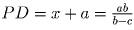 .
Далее, из подобия треугольников AMQ и PCQ следует
.
Далее, из подобия треугольников AMQ и PCQ следует
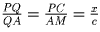 . Утверждение задачи следует из равенства
. Утверждение задачи следует из равенства
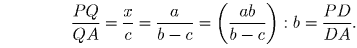
iv01.93
Задача 4: Мишень представляет собой треугольник, разбитый тремя семействами параллельных прямых на 100 равных правильных треугольничков с единичными сторонами. Снайпер стреляет по мишени. Он целится в треугольничек и попадает либо в него, либо в один из соседних с ним по стороне. Он видит результаты своей стрельбы и может выбирать, когда стрельбу заканчивать. Какое наибольшее число треугольничков он может с гарантией поразить ровно пять раз.(Ю.Лифшиц)
Решение: Ответ: 25. I) Стратегия: рассмотрим разбиение мишени на 25 треугольных кусков 2 × 2, т.е. состоящие из четырех треугольников (см. рис.). Тогда стреляя в центр каждого из них до тех пор, пока в одном из четырех треугольников куска не накопится пять попаданий, он получит ровно 25 «призовых мишеней». II) Если при стрельбе в какой-то треугольничек какого-то куска стрелок всегда будет попадать в центральный треугольничек этого куска, то «призовых» мишеней будет не больше 25-и, т.к. в остальные он не попадет ни разу.iv01.84
Задача 5: В выпуклом пятиугольнике выбраны две точки. Докажите, что можно выбрать четырехугольник с вершинами в вершинах пятиугольника так, что в него попадут обе выбранные точки.
(В.Дольников)
Решение: Решение 1. Рассмотрим в нашем пятиугольнике ABCDE 5 треугольников: ABC, BCD, CDE, DEA, EAB (см. рис.).Тогда любая точка лежит не более, чем в двух треугольниках, следовательно есть треугольник, в котором нет наших точек. Отрезаем его и получаем разрез, удовлетворяющий условию.
Решение 2. Проведем прямую через эти точки. В одной из полуплоскостей лежит три вершины пятиугольника (из которых хотя бы две не лежат на этой прямой). Отрезаем этот треугольник и получаем нужное разбиение.
iv01.95
Задача 6: Существует ли такое натуральное число, что произведение всех его натуральных делителей (включая 1 и само число) оканчивается ровно на 2001 ноль?
(А.Храбров)
Решение: Ответ: Существует. Например, 5 • 2²ººº или 2 • 5²ººº.Покажем, что первое число подходит. Для этого выпишем все его делители, кратные пяти:
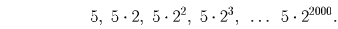
(С.Берлов, П.Кожевников)
Решение: Пусть ∠ OAK = α . Из параллельности LK || OA следует: ∠ LKM = ∠ OAK = α . По теореме об угле между касательной и хордой: ∠ KBA = ∠ OAK = α . Так как углы LKM и LBM вписаны в окружность ω и опираются на одну дугу, то ∠ LBM = ∠ LKM = α .Из равенства углов ∠ OAM = ∠ OBM = α следует, что четырехугольник OABM — вписанный. Отсюда ∠ OMA = ∠ OBA. Но ∠ OBA = ∠ KBM, так как ∠ KBA = ∠ OBM = α . Значит, ∠ OMA = ∠ KBM, откуда по обратной теореме о касательной и хорде получаем, что OM касается окружности ω в точке M.
iv01.97
Задача 8: Саша написал на доске ненулевую цифру и приписывает к ней справа по одной ненулевой цифре, пока не выпишет миллион цифр. Докажите, что на доске не более 100 раз был написан точный квадрат.
(А.Голованов)
Решение: Рассмотрим отдельно числа из нечетного и из четного числа знаков. Пусть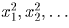 — встретившиеся на доске
квадраты из четного количества знаков, и в их записи содержится соответственно
2n1,2n2, … (n1 < n2 < … ) цифр. Аналогично, пусть
— встретившиеся на доске
квадраты из четного количества знаков, и в их записи содержится соответственно
2n1,2n2, … (n1 < n2 < … ) цифр. Аналогично, пусть 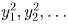 — встретившиеся на доске квадраты из нечетного количества
знаков, и в их записи содержится соответственно 2m1 – 1,2m2 – 1, … (m1 < m2 < … ) цифр.
— встретившиеся на доске квадраты из нечетного количества
знаков, и в их записи содержится соответственно 2m1 – 1,2m2 – 1, … (m1 < m2 < … ) цифр.Число 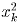 содержит nk цифр и не оканчивается на 0, поэтому
содержит nk цифр и не оканчивается на 0, поэтому
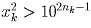 , откуда
, откуда 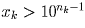 . Число
. Число 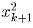 получается из xk приписыванием некоторого четного количества –
обозначим его 2a — ненулевых цифр.
Поэтому
получается из xk приписыванием некоторого четного количества –
обозначим его 2a — ненулевых цифр.
Поэтому 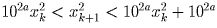 .
Из левого неравенства получаем
10axk + 1 ≤ xk + 1, следовательно,
.
Из левого неравенства получаем
10axk + 1 ≤ xk + 1, следовательно,
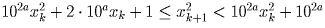 , откуда
2 • 10axk + 1 < 102a, т.е. xk < 10a.
Из этого неравенства следует, что xk содержит не более a цифр, т.е.
nk ≤ a, тогда из неравенства 10axk + 1 ≤ xk + 1 следует
a + nk ≤ nk + 1, откуда 2nk ≤ nk + 1.
, откуда
2 • 10axk + 1 < 102a, т.е. xk < 10a.
Из этого неравенства следует, что xk содержит не более a цифр, т.е.
nk ≤ a, тогда из неравенства 10axk + 1 ≤ xk + 1 следует
a + nk ≤ nk + 1, откуда 2nk ≤ nk + 1.
Аналогичное рассуждение применимо к последовательности yk:
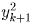 получается приписыванием к
получается приписыванием к 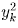 2a цифр, yk < 10a,
и a ≥ mk, то есть mk + 1 ≥ 2mk. Теперь заметим, что
в каждой из последовательностей mk и nk меньше 50 членов (так
как m1,n1 ≥ 1 и m50 и n50 должны быть не меньше,
чем 250 > 1000000).
2a цифр, yk < 10a,
и a ≥ mk, то есть mk + 1 ≥ 2mk. Теперь заметим, что
в каждой из последовательностей mk и nk меньше 50 членов (так
как m1,n1 ≥ 1 и m50 и n50 должны быть не меньше,
чем 250 > 1000000).
Итак, всего квадратов на доске окажется не более 100.
| Задачная база >> Соревнования всероссийского уровня >> Зональный этап всероссийской олимпады. >> XXVII >> 9 класс | Убрать решения |