 |
 |
|
| Задачная база >> Украинские соревнования >> Харьковские соревнования >> Областные олимпиады >> 1990 >> 10 класс | Показать решения |
|
|
| Харьковские областные олимпиады. 1990. 10 класс |
|
|
Решить уравнение
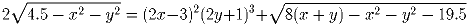
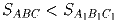
Задача 4:
Задача 5: Даны окружность, точка M на ней и диаметр AB. С помощью одной линейки опустить из точки M перпендикуляр на AB. (M ≠ A, M ≠ B).
| Задачная база >> Украинские соревнования >> Харьковские соревнования >> Областные олимпиады >> 1990 >> 10 класс | Показать решения |