Задача 1: Числа x и y положительны и x + y = 1. Какое наименьшее значение может иметь выражение ...

Задача 2: Пусть AE и BD – высоты остроугольного треугольника ABC, причем DE\|AB. Доказать, что  ∆ ABC равнобедренный.

Задача 3: Решить систему неравенств:

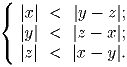
Задача 4: На циферблате часов расположены 1990 точек. Доказать, что найдется момент времени, начиная с которого в течение 200 секунд минутная стрелка «заметет" хотя бы 111 точек.

Задача 5: а) В бесконечной последовательности натуральных чисел каждый член, начиная со второго, получается из предыдущего приписыванием в конце какой-либо цифры, отличной от 3 и 9. Доказать, что в этой последовательности найдется бесконечно много составных чисел.

б) то же самое, но разрешается приписывать цифру 3.