Задача 1:
Найти площадь фигуры, ограниченной графиками функций y = π x и
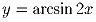
.
Задача 2:
Задача 3:
Натуральные числа m и n удовлетворяют условию m ≤ n ≤ 100. Доказать, что в десятичной записи дроби
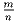
не
встречается последовательность цифр …167… .
Задача 4:
Среди числовых последовательностей
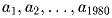
удовлетворяющих условию a
i = a
i + 10 для всех 1 ≤ i ≤ 1970, найти такую, для которой выражение (a
1 – 1)² + (a
2 – 2)² + … + (a
1980 – 1980)² принимает наименьшее возможное значение.
Задача 5:
Обозначим a
n наибольшее значение функции f(x) = sin x – x
n на множестве [\,0; ∞ ). Найти
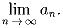
Задача 6:
На сфере радиуса R размещены четыре окружности одинакового
радиуса, попарно касающиеся друг друга. Найти радиус этих
окружностей.
Задача 7:
В окружность единичного радиуса вписан 2n-угольник
A
1A
2 … A
2n. Доказать, что длина вектора
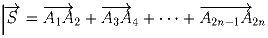
всегда
меньше 2.
Задача 8:
В шахматном турнире принимало участие n ≥ 3 шахматистов,
каждые два из которых сыграли между собой одну партию. После
окончания турнира оказалось, что для каждых двух участников,
сыгравших между собой не вничью, общее число сделанных ими ничьих не
меньше n. Доказать, что участников турнира можно рассадить за
круглым столом так, чтобы соседями каждого шахматиста были люди,
сыгравшие с ним вничью.


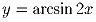 .
.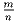 не
встречается последовательность цифр …167… .
не
встречается последовательность цифр …167… .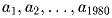 удовлетворяющих условию ai = ai + 10 для всех 1 ≤ i ≤ 1970, найти такую, для которой выражение (a1 – 1)² + (a2 – 2)² + … + (a1980 – 1980)² принимает наименьшее возможное значение.
удовлетворяющих условию ai = ai + 10 для всех 1 ≤ i ≤ 1970, найти такую, для которой выражение (a1 – 1)² + (a2 – 2)² + … + (a1980 – 1980)² принимает наименьшее возможное значение.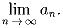
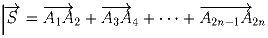 всегда
меньше 2.
всегда
меньше 2.