Задача 1:
Найти на координатной плоскости такие точку F и прямую
l, чтобы каждая точка параболы y = x² находилась на равных
расстояниях от F и l.
Задача 2:
Вектор
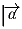
имеет единичную длину и рациональные
координаты. Доказать, что среди перпендикулярных к
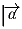
векторов единичной длины найдётся вектор с рациональными
координатами.
Задача 3:
Квадратные уравнения x² + ax + b = 0 и x² + cx + d = 0 имеют
положительные дискриминанты, причём (b – d)² – (a – c)(bc – ad) < 0.
Доказать, что между корнями одного из уравнений содержится точно один
корень второго уравнения.
Задача 4:
Два игрока по очереди переставляют фишку по координатной
плоскости. В начальный момент фишка находится в точке O(0;0). За
один ход разрешается передвинуть фишку на единицу по горизонтали или
вертикали клеток, причём повторение предыдущего хода в
противоположном направлении запрещено. Игрок A начинает игру и
старается отодвинуть пешку как можно дальше от начала координат, а
игрок B стремится придвинуть пешку как можно ближе к началу. На
каком расстоянии от начальной клетки окажется пешка, если каждый из игроков
сделает по 2n ходов и будет действовать наилучшим образом?
Задача 5:
Множество точек

отрезка AB симметрично
относительно середины этого отрезка. Какие-то n из них покрашены в
синий цвет, а остальные — в красный. Доказать, что сумма расстояний
от всех красных точек до точки A равняется сумме расстояний от всех
синих точек до точки B.
Задача 6: 7. Город имеет 8 улиц, идущих с юга на север, и 8, идущих с
востока на запад. Пересекаясь, они образуют 64 перекрёстка. Служба
точного времени хочет установить на некоторых перекрёстках часы так,
чтобы на каждом перекрёстке можно было видно хотя бы двое часов на
других перекрёстках (с перекрёстка просматриваются обе улицы,
проходящие через него, однако на каждой улице с каждой стороны видны
только ближайшие часы). Какое наименьшее количество часов требуется
для этого?
Задача 8:
Доказать, что в треугольной пирамиде, высоты которой
пересекаются в одной точке, все три плоских угла при каждой вершине
пирамиды либо одновременно острые, либо прямые, либо тупые.


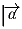 имеет единичную длину и рациональные
координаты. Доказать, что среди перпендикулярных к
имеет единичную длину и рациональные
координаты. Доказать, что среди перпендикулярных к 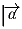 векторов единичной длины найдётся вектор с рациональными
координатами.
Задача 3:
Квадратные уравнения x² + ax + b = 0 и x² + cx + d = 0 имеют
положительные дискриминанты, причём (b – d)² – (a – c)(bc – ad) < 0.
Доказать, что между корнями одного из уравнений содержится точно один
корень второго уравнения.
векторов единичной длины найдётся вектор с рациональными
координатами.
Задача 3:
Квадратные уравнения x² + ax + b = 0 и x² + cx + d = 0 имеют
положительные дискриминанты, причём (b – d)² – (a – c)(bc – ad) < 0.
Доказать, что между корнями одного из уравнений содержится точно один
корень второго уравнения. отрезка AB симметрично
относительно середины этого отрезка. Какие-то n из них покрашены в
синий цвет, а остальные — в красный. Доказать, что сумма расстояний
от всех красных точек до точки A равняется сумме расстояний от всех
синих точек до точки B.
отрезка AB симметрично
относительно середины этого отрезка. Какие-то n из них покрашены в
синий цвет, а остальные — в красный. Доказать, что сумма расстояний
от всех красных точек до точки A равняется сумме расстояний от всех
синих точек до точки B.