 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1981, Симферополь >> 8 класс | Показать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1981, Симферополь. 8 класс |
|
|
Задача 2: Доказать, что два прямоугольника с параллельными сторонами подобны тогда и только тогда, когда одна из диагоналей одного прямоугольника параллельна или перпендикулярна одной из диагоналей второго.
Задача 3: Доказать, что множество чисел 1414 можно разбить на подмножества так, чтобы сумма чисел в каждом подмножестве была равна 1981.
Задача 4: Найти сторону наименьшего квадрата, в котором можно разместить без наложений три круга радиусов 1,
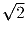 и 2.
и 2.Задача 5: Внутри данного угла LMN заданы две точки A и B. Построить параллелограмм, у которого две противоположные вершины — точки A и B, а две другие лежат на сторонах угла LMN.
Задача 6: Можно ли расположить по окружности цифры от 0 до 9 включительно так, чтобы сумма любых трёх стоящих рядом цифр не превышала: а) 14; б) 15?
Задача 7: В автомат кидают медные монеты на сумму n копеек. Пусть an — количество способов, которыми это можно сделать (с учётом порядка вбрасывания монет разной стоимости). Например, сумму в 3 копейки можно кинуть четырьмя способами: 3, 1+2, 2+1 и 1+1+1, поэтому a3 = 4; аналогично a4 = 7 и т.д. Доказать, что начиная с некоторого места, последняя цифра чисел an будет периодически повторяться.
Задача 8: Доказать, что для произвольных чисел p и q сумма длин отрезков оси Ox, для точек которых выполняется неравенство |x² + px + q| ≤ 2, не превышает 4.
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1981, Симферополь >> 8 класс | Показать решения |