 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1981, Симферополь >> 9 класс | Показать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1981, Симферополь. 9 класс |
|
|
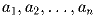 выполняется неравенство
выполняется неравенство

Задача 2: Из вершин A и A1 куба ADCBA1B1C1D1 вдоль его рёбер начинают двигаться с одинаковой скоростью точки P и P1. Точка P движется вдоль контура ABCDA, а точка P1 — вдоль контура A1D1C1B1A1. С какой скоростью и по какой траектории движется при этом середина отрезка PP1?
Задача 3: Точка с координатами (x(t);y(t)) движется в координатной плоскости xOy так, что в каждый момент времени t выполняются равенства:
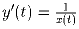 ,
, 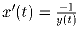 . Известно, что в некоторый момент времени точка
имела координаты (12;3). Может ли эта точка в некоторый другой момент
времени иметь координаты (6;5)?
. Известно, что в некоторый момент времени точка
имела координаты (12;3). Может ли эта точка в некоторый другой момент
времени иметь координаты (6;5)?Задача 4: После возведения в степень и приведения подобных членов число
 приводится к виду
приводится к виду  , где a и b —
целые числа. Доказать, что a и b делятся на 21980.
, где a и b —
целые числа. Доказать, что a и b делятся на 21980.Задача 5: Последовательности an и bn заданы реккуррентными соотношениями

Задача 6: Прямой угол перемещается в координатной плоскости xOy так, что его стороны касаются параболы y = ax² (a > 0). Какую траекторию при этом описывает вершина прямого угла?
Задача 7: Найти все многочлены вида xn + a1xn – 1 + … + an – 1x + an, где |ai| = 1, i = n, которые имеют n действительных корней.
Задача 8: Для квадратной таблицы (2n + 1) × (2n + 1), заполненной числами – 1, 0 и 1, вычислили сумму чисел каждого столбца и каждой строки. Доказать, что среди этих сумм хотя бы две будут одинаковыми.
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1981, Симферополь >> 9 класс | Показать решения |