Задача 1: Числа a, b, c удовлетворяют равенству

Чему может быть равно число

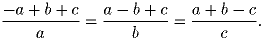
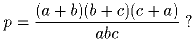
Задача 2: Одна из сторон правильного треугольника поделена на 50 равных частей и через точки деления проведены прямые, параллельные другой стороне. Эти прямые разбивают данный треугольник на 49 трапеций и один треугольник. Найти отношение площади самой большой трапеции к площади самой маленькой трапеции.

Задача 3: Во время игры в домино возникла позиция, когда ни один из игроков не может сделать ход. Какое наибольшее число косточек может при этом остаться у игроков?

Задача 4: Найти все пятизначные числа 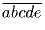, которые делятся на .

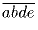Задача 5: Дан произвольный треугольник ABC. Найти множество точек M таких, что

где A₁, B₁, C₁ — соответственно точки на сторонах BC, AC, AB треугольника такие, что

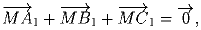
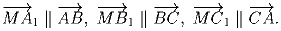
Задача 6: Сумма четырёх чисел равна нулю, а модуль каждого из них не больше 1. Доказать, что сумма некоторых двух из них не превышает по модулю ⅔.