 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1982, Николаев >> 9 класс | Показать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1982, Николаев. 9 класс |
|
|
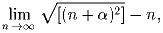
Задача 2: На плоскости даны правильный шестиугольник и вектор
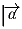 .
Найти сумму ортогональных проекций вектора
.
Найти сумму ортогональных проекций вектора 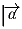 на стороны шестиугольника
или на их продолжения.
на стороны шестиугольника
или на их продолжения.Задача 3: Найти наибольшее натуральное n, для которого система неравенств
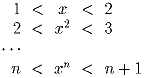
Задача 4: На бумажной ленте записана последовательность из 360 цифр 123123…123123…123. На какое наибольшее число частей можно разрезать эту ленту, чтобы все числа на полученных при этом кусочках ленты были различными?
Задача 5: В теннисном турнире принимали участие n женщин и 2n мужчин. Все участники турнира сыграли между собой по одному разу. Известно, что отношение числа побед, одержанных женщинами, к числу побед, одержанных мужчинами (ничьих не бывает), равно
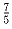 . Найти n.
. Найти n.Задача 6: В остроугольном треугольнике ABC высоты пересекаются в точке H. Пусть AB = c, AC = b, BC = a, AH = x, BH = y, CH = z. Доказать, что abc = ayz + bxz + cxy.
Задача 7: Существуют ли арифметическая
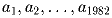 и геометрическая
и геометрическая
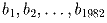 прогресии, для которых выполняются неравенства
a1 < b1 < a2 < b2 < … < a1982 < b1982 ?
прогресии, для которых выполняются неравенства
a1 < b1 < a2 < b2 < … < a1982 < b1982 ?Задача 8: Модуль каждого из 100 чисел не превосходит 1, а их сумма равна нулю. Доказать, что:
а) Эти числа можно разбить на 10 групп по 10 чисел в каждой группе так, чтобы модуль суммы чисел в каждой группе не превышал 2;
б) Число 2 в предыдущем пункте нельзя заменить на 1.
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1982, Николаев >> 9 класс | Показать решения |