Задача 1:
Задача 2:
В некоторых клетках шахматной доски размера n × n,
n > 1, установлены лампочки. Известно, что каждые 4 клетки доски с
общей вершиной содержат чётное число лампочек (то есть 0, 2 или
4). Доказать, что четыре угловые клетки доски тоже содержат чётное
число лампочек.
Задача 3:
Внутри треугольника ABC выбрана точка O и через неё
проведены прямые OA, OB, OC до пересечения со сторонами BC,
AC, AB в точках A
1, B
1, C
1 соответственно. Доказать, что
сумма OA
1 + OB
1 + OC
1 меньше наибольшей из сторон треугольника
ABC.
Задача 4:
На круге последовательно через 120 записаны числа 1,
2 и 3. Круг прикреплен к доске так, что он может поворачиваться
вокруг своего центра на углы, кратные 120. Вначале рядом с
каждым числом 1, 2 и 3 на доске написан нуль. Разрешается
поворачивать круг несколько раз и после каждого поворота к каждому из
написанных на доске чисел прибавить то число, которое оказалось рядом
с ним на круге. Можно ли в результате получить на доске записанные по
ходу часовой стрелки числа 11, 11, 14?
Задача 5:
Дан шестиугольник ABCDEF. Доказать, что его периметр P
больше, чем ⅔(AD + BE + CF).
Задача 6:
Вдоль дороги расставлены светофоры на расстоянии 1 км друг от
друга. В течение 1 минуты с начала каждого часа на них загорается красный свет,
запрещая проезд, а остальное время горит зеленый свет. Мотоциклист начинает
движение с постоянной скоростью у светофора, на котором только что загорался
красный свет и за 10 часов пути ни разу не встретил красного света (ни разу не
затормозил). Какое наибольшее расстояние он мог проехать за это время?
Задача 7:
Какое наибольшее значение может принимать разность
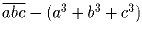
(разность трёхзначного числа
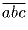
и суммы
кубов его цифр)?
Задача 8:
Каждую грань куба разбили на 4 одинаковых квадрата и каждый из
получившихся квадратов покрасили одной из имеющихся 3 красок. Доказать, что
если квадраты с общим ребром покрашены в разные цвета, то всего имеется по 8
квадратов каждого цвета. Привести пример такой раскраски.


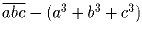 (разность трёхзначного числа
(разность трёхзначного числа 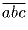 и суммы
кубов его цифр)?
и суммы
кубов его цифр)?