Задача 1:
Найти сумму всех натуральных чисел от 1 до 1000, не делящихся
на 7.
Задача 2:
Две окружности равных радиусов касаются в точке A.
Окружность удвоенного радиуса содержит внутри себя одну из данных
окружностей, касаясь её в точке B, а другую пересекает в точках P
и Q. Доказать, что прямая AB проходит или через точку P, или
через точку Q.
Задача 3:
Доказать, что к графику функции y = x³ можно провести три
касательные, пересекающихся в одной точке.
Задача 4:
На плоскости даны такие точки
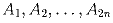
и точка B, что
если точку B симметрично отразить последовательно относительно
точек
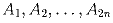
(то есть сначала отобразить точку B в
симметричную ей относительно A
1 точку B
1, затем точку B
1
отобразить в симметричную ей относительно A
2 точку B
2 и т.д.),
то снова получим точку B (то есть точка B
2n совпадает с точкой
B). Доказать, что если произвольную точку M плоскости симметрично
отразить последовательно относительно точек A
2, A
3, …, A
2n,
A
1, то получим саму точку M.
Задача 5:
Доказать, что из равенств ac – a – c = b² – 2b и bd – b – d = c² – 2c
следует равенство ad + b + c = bc + a + d.
Задача 6:
Задача 7:
а) Какое наименьшее количество чисел может содержать набор
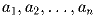
, если в нём все числа различны и каждое из них: а) равно произведению двух других чисел из этого набора; б) равно сумме двух других чисел из этого набора.
Задача 8:
На плоскости взяты 1984 точки, никакие три из которых не
лежат на одной прямой. Каждые 2 точки соединим отрезком и зафиксируем
на нём одно из двух направлений. По каждому отрезку можно двигаться
только в выбранном направлении. Доказать, что среди взятых точек
найдётся такая, из которой можно попасть в любую другую точку, пройдя
не более двух отрезков.


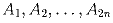 и точка B, что
если точку B симметрично отразить последовательно относительно
точек
и точка B, что
если точку B симметрично отразить последовательно относительно
точек 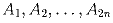 (то есть сначала отобразить точку B в
симметричную ей относительно A1 точку B1, затем точку B1
отобразить в симметричную ей относительно A2 точку B2 и т.д.),
то снова получим точку B (то есть точка B2n совпадает с точкой
B). Доказать, что если произвольную точку M плоскости симметрично
отразить последовательно относительно точек A2, A3, …, A2n,
A1, то получим саму точку M.
(то есть сначала отобразить точку B в
симметричную ей относительно A1 точку B1, затем точку B1
отобразить в симметричную ей относительно A2 точку B2 и т.д.),
то снова получим точку B (то есть точка B2n совпадает с точкой
B). Доказать, что если произвольную точку M плоскости симметрично
отразить последовательно относительно точек A2, A3, …, A2n,
A1, то получим саму точку M.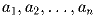 , если в нём все числа различны и каждое из них: а) равно произведению двух других чисел из этого набора; б) равно сумме двух других чисел из этого набора.
, если в нём все числа различны и каждое из них: а) равно произведению двух других чисел из этого набора; б) равно сумме двух других чисел из этого набора.