 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1986, Ровно >> 7 класс | Показать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1986, Ровно. 7 класс |
|
|
Задача 2: Найти окружность наименьшего радиуса, в которую можно поместить фигуру, изображённую на рисунке (сторона каждого квадрата равна 1).
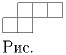
Задача 3: Построить замкнутую ломаную, каждые два соседних звена которой взаимно перпендикулярны, и которая имеет 10 звеньев и 7 точек самопересечения.
Задача 4: Вершины куба занумерованы числами 8 в произвольном порядке. Доказать, что всегда найдётся грань, сумма номеров вершин которой не меньше 18. Всегда ли найдётся грань, для которой сумма номеров вершин не меньше 19?
Задача 5: Построить треугольник, если даны две его вершины A и B и прямые, на которых лежат медиана и биссектриса, проведенные из вершины A.
Задача 6: На доске выписали натуральные числа от 1 до 1 000 000. Затем каждое число заменили суммой его цифр. С каждым полученным числом сделали то же самое. И так до тех пор, пока на доске не останутся лишь однозначные числа. Каких чисел получится больше — единиц или двоек?
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1986, Ровно >> 7 класс | Показать решения |