Задача 1:
Вычислить
cos \,( π \, cos \,(2 π \, cos \,(3 π \, cos … \,(1985 π \, cos \,(1986 π ) … ).
Задача 2:
Задача 3:
Через точку O внутри выпуклого четырёхугольника ABCD
проведены четыре разных окружности одинакового радиуса, каждая из
которых касается двух смежных сторон четырёхугольника. Доказать, что
вокруг четырёхугольника ABCD можно описать окружность.
Задача 4:
Дано действительное число
α = 0, α
1 α
2 … α
n … \,. Образуем такую
последовательность: a
1 = α ,
a
2 = 0, α
2 α
3 … α
n … \,, …,
a
n = 0, α
n α
n + 1 … , …(каждое следующее число получается из
предыдущего вычёркиванием первой цифры после запятой). Известно, что
последовательность a
n сходящаяся. Доказать, что число α —
рациональное.
Задача 5:
О числах
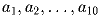
известно, что
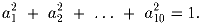
Доказать, что
a
1a
2 + a
2a
3 + … + a
9a
10 + a
10a
1 ≥ – 1.
Может ли здесь достигаться равенство?
Задача 6:
В выпуклом 1986-угольнике проведены несколько диагоналей так,
что любая из них пересекает внутри многоугольника не более одной
диагонали из числа проведенных. Какое наибольшее число диагоналей
можно провести?
Задача 7:
Из точки M, взятой на стороне BC правильного треугольника
ABC, проведены перпендикуляры MN и MK к сторонам AB и AC
соответственно. Обозначим через O центр треугольника ABC, а
через P — точку пересечения отрезков KN и OM. Доказать, что
NP = PK.
Задача 8:
Многочлен четвертой степени P(x) имеет четыре различных
корня: a > b > c > d. Известно, что P(x) можно представить в виде
P(x) = Q(R(x)), где Q(x) и R(x) — квадратные трёхчлены.
Доказать, что a – b = c – d.


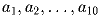 известно, что
известно, что