 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1987, Тернополь >> 10 класс | Показать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1987, Тернополь. 10 класс |
|
|
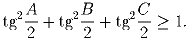
Задача 3: Найти целую часть числа

Задача 4: Доказать, что каждая плоскость, проходящая через середины двух противоположных рёбер треугольной пирамиды, делит её на две одинаковые по объёму части.
Задача 5: Какие значения может принимать число x, если выполнены такие равенства:
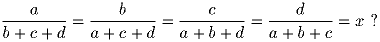
Задача 6: Через вершины A1, A2 и A3 треугольника A1A2A3 соответственно провели три разных параллельных прямых l1, l2 и l3. Пусть Bi, i = 1, 2, 3 — точка пересечения прямой li с противоположной вершине Ai стороной треугольника (или её продолжением). Найти отношение площади треугольника A1A2A3 к площади треугольника B1B2B3.
Задача 7: Известно, что натуральное число n не является точной четвертой степенью. Доказать, что дробная часть числа
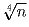 удовлетворяет неравенству
удовлетворяет неравенству 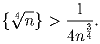
Задача 8: По окружности выписаны числа
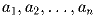 , сумма которых равна
1. С этими числами разрешается делать такие
преобразования: если подряд идёт несколько отрицательных чисел
, сумма которых равна
1. С этими числами разрешается делать такие
преобразования: если подряд идёт несколько отрицательных чисел
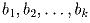 , причём
, причём 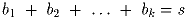 , то числа b0,
, то числа b0, 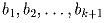 можно заменить соответственно на числа b0 + s, – bk, – bk – 1,
…, – b2, – b1, b0 + s. Например, числа …, 1, 7, -3,
-5, -2, 3, …можно заменить числами …, 1, -3, 2, 5, 3, -7,
…(b1 = – 3, b2 = – 5, b3 = – 2, s = – 10), или числами …, 1,
7, -10, 5, 2, -4, …(b1 = – 5, b2 = – 2) и т.д. Доказать, что
такие преобразования нельзя делать сколь угодно долго (то есть рано
или поздно в результате преобразований не останется ни одного
отрицательного числа).
можно заменить соответственно на числа b0 + s, – bk, – bk – 1,
…, – b2, – b1, b0 + s. Например, числа …, 1, 7, -3,
-5, -2, 3, …можно заменить числами …, 1, -3, 2, 5, 3, -7,
…(b1 = – 3, b2 = – 5, b3 = – 2, s = – 10), или числами …, 1,
7, -10, 5, 2, -4, …(b1 = – 5, b2 = – 2) и т.д. Доказать, что
такие преобразования нельзя делать сколь угодно долго (то есть рано
или поздно в результате преобразований не останется ни одного
отрицательного числа).
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1987, Тернополь >> 10 класс | Показать решения |