 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1987, Тернополь >> 9 класс | Показать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1987, Тернополь. 9 класс |
|
|
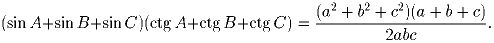
Задача 2: Доказать, что существует такое целое n < 109, что первые 7 цифр дробной части числа n π будут нулями.
Задача 3: Доказать, что для произвольных действительных чисел a,b,c выполняется неравенство: a • 2 – a + b • 2 – b + c • 2 – c ≤ a • 2 – b + b • 2 – c + c • 2 – a.
Задача 4: Доказать, что для каждого нечётного натурального числа n существует пространственное тело, имеющее ровно n осей симметрии. Если пространственное тело имеет оси симметрии, может ли их количество быть чётным?
Задача 5: Известно, что уравнение x¹² – abx + a² = 0 имеет корень x0 > 2. Доказать, что |b| > 64.
Задача 6: Известно, что натуральное число n не является точным квадратом. Доказать, что дробная часть числа
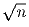 удовлетворяет неравенству
удовлетворяет неравенству 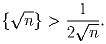
Задача 7: Для каких натуральных чисел n из каждого набора n² чисел
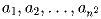 можно выбрать монотонную подпоследовательность длины n + 1 (то
есть такую последовательность чисел
можно выбрать монотонную подпоследовательность длины n + 1 (то
есть такую последовательность чисел 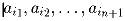 , i1 < i2 < … < in + 1, которая удовлетворяет условию ai1 ≤ ai2 ≤ … ≤ ain + 1 или условию ai1 ≥ ai2 ≥ … ≥ ain + 1)?
, i1 < i2 < … < in + 1, которая удовлетворяет условию ai1 ≤ ai2 ≤ … ≤ ain + 1 или условию ai1 ≥ ai2 ≥ … ≥ ain + 1)?Задача 8: На сторонах треугольника ABC вне его построили квадраты AA2B1B, BB2C1C и CC2A1A. Доказать, что серединные перпендикуляры к отрезкам A1A2, B1B2 и C1C2 пересекаются в одной точке.
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1987, Тернополь >> 9 класс | Показать решения |