Задача 1: На бесконечной шахматной доске расставлены несколько ферзей так, что каждый из них бьет ровно K других ферзей. Доказать, что K ≤ 4.

Задача 2: В треугольнике ABC обозначим через K и L точки касания со стороной AB соответственно вписанной и вневписанной окружностей. Доказать, что AL = BK.

Задача 3:

Задача 4:

3ptto8pt.1pt to8pt.1ptto8pt. Число

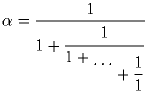
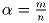(черта дроби встречается в правой части 1988 раз) записано в виде обычной несократимой дроби . Доказать, что

Задача 5: Для каждой параболы y = x² + px + q, график которой пересекает оси координат в трёх различных точках, проводим через эти точки окружность. Доказать, что существует точка, через которую проходит каждая из этих окружностей.

Задача 6: Через произвольную точку L, взятую на стороне AB треугольника ABC, проведена параллельно стороне AC прямую, пересекающую сторону BC в точке M. Потом через точку M проведена параллельно стороне AB прямая, пересекающая сторону AC в точке N. Какое наибольшее значение может принимать отношение площади треугольника LMN к площади треугольника ABC?

Задача 7:

Задача 8: Перед началом игры на некоторых клетках шахматной доски размером 10 × 10 расставлены 12 фишек. Каждым ходом ставятся новые фишки на все те клетки, для которых хотя бы две соседние уже заняты фишками (соседними считаются клетки, имеющие общую сторону).

а) Доказать, что можно так расставить фишки перед началом игры, что игра закончится не раньше, чем через 41 ход.

б) Можно ли расставить фишки перед началом игры так, чтобы игра продолжалась не менее 61 хода?