Задача 1:
На каждой клетке доски размерами 9 × 9 сидит жук. По сигналу
каждый жук переползает в одну из соседних по диагонали клеточек (см.рис.). При
этом может оказаться, что в некоторых клетках будет по нескольку жуков, а
некоторые клетки будут свободными. Найти наименьшее возможное число свободных
клеток.

Задача 2:
Дан равносторонний треугольник ABC. С центром в точке A радиусом
AB описана дуга BC. Пусть M — произвольная точка дуги BC, отличная от
B и C. Середины хорд MC и MB соединены отрезками соответственно с
серединами сторон AB и AC. Доказать, что построенные отрезки взаимно
перпендикулярны.
Задача 3:
Среди всех треугольников, которые отсекаются от координатных осей Ox,
Oy касательными к окружности x² + y² = a², найти тот, который имеет
наименьшую площадь.
Задача 4:
Найти все пары натуральных чисел, которые обладают таким свойством:
если к любому из них прибавить 1, то оно разделится на другое.
Задача 5:
Доказать, что если
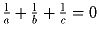
, то
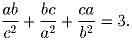
Задача 6:
Две вершины треугольника закреплены в точках A и B, а третья
вершина C перемещается в плоскости так, что разность расстояний от неё до
точек A и B постоянна. Доказать, что центры окружностей, вписанных в
треугольники ABC, лежат на одной прямой.



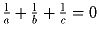 , то
, то