Задача 1:
Можно ли накрыть квадрат 6 × 6 тремя квадратами 5 × 5?
Задача 2:
Задача 3:
Рассматривается сумма всех векторов
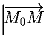
с общим
началом в точке M
0 и концами в точках M, лежащих в квадрате
– 994 ≤ x ≤ 994, – 994 ≤ y ≤ 994 и имеющих целые
координаты. Указать наибольшее и наименьшее возможные значения длины
суммы таких векторов в зависимости от положения точки M
0 (точка
M
0 также лежит в квадрате).
Задача 4:
Среди всех треугольников, которые отсекаются от координатных
осей Ox и Oy касательными к окружности x² + y² = a² , найти тот,
который имеет наименьший периметр.
Задача 5:
Найти все тройки натуральных чисел, обладающих следующим
свойством: произведение любых двух из них в сумме с 1 делится на
третье число.
Задача 6:
Изобразить область
D = (x,y):2|x| + |y + 2x + 1| ≤ 5
и вычислить её площадь.
Задача 7:
В окружности провели два диаметра AB и CD. Пусть M —
произвольная точка окружности, не совпадающая ни с одной из точек A, B,
C, D, а M
1 и M
2 — проекции точки M на диаметры AB и CD
соответственно. Доказать, что длина отрезка M
1M
2 не зависит от положения
точки M.
Задача 8:


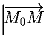 с общим
началом в точке M0 и концами в точках M, лежащих в квадрате
– 994 ≤ x ≤ 994, – 994 ≤ y ≤ 994 и имеющих целые
координаты. Указать наибольшее и наименьшее возможные значения длины
суммы таких векторов в зависимости от положения точки M0 (точка
M0 также лежит в квадрате).
с общим
началом в точке M0 и концами в точках M, лежащих в квадрате
– 994 ≤ x ≤ 994, – 994 ≤ y ≤ 994 и имеющих целые
координаты. Указать наибольшее и наименьшее возможные значения длины
суммы таких векторов в зависимости от положения точки M0 (точка
M0 также лежит в квадрате).