 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1990, Днепропетровск >> 11 класс | Показать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1990, Днепропетровск. 11 класс |
|
|
Задача 2: В каком наибольшем конечном числе точек прямая может касаться синусоиды?
Задача 3: Доказать, что шахматную доску размером 1989 × 1991 с вырезанной центральной клеткой нельзя обойти ладьей, побывав на каждой клетке ровно один раз.
Задача 4: В правильном тетраэдре ABCD на грани ABC взята точка M так, что радиусы сфер, описанных около тетраэдров DABM, DACM и DBCM, одинаковы. Доказать, что DM — высота тетраэдра ABCD.
Задача 5: В пространстве даны несколько векторов. Известно, что длина суммы любых двух векторов не больше 2. Доказать, что длина суммы любых трёх векторов не больше 3.
Задача 6: На плоскости даны две окружности, пересекающиеся в двух точках A и B. Одна из окружностей проходит через центр другой. Через точку A проведем прямую, которая пересекает первую окружность ещё раз в точке M, а вторую — в точке N. Доказать, что треугольник MNB — равнобедренный.
Задача 7: Доказать, что для любых положительных чисел a, b и c выполняется неравенство:
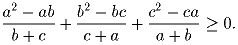
Задача 8: В группе, составленной из n лиц, у каждого не меньше, чем m знакомых (n ≥ 2m). Доказать, что в этой группе можно выделить m разных пар попарно знакомых людей. (Каждый человек может входить не более чем в одну из выделенных пар).
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1990, Днепропетровск >> 11 класс | Показать решения |