Задача 1:
Доказать, что для любых неотрицательных чисел a и b
выполнено неравенство a³ + 2b³ > 3ab².
Задача 2:
Задача 3:
Натуральные числа 1990 в порядке возрастания
записаны по окружности по часовой стрелке. Будем при каждом обходе,
начиная с 1 и двигаясь по часовой стрелке, зачеркивать каждое второе
из чисел, не зачеркнутых раньше, до тех пор, пока не останется одно
число. Какое число останется?
Задача 4:
В четырёхугольнике ABCD углы BAD и ABC равны по
100, а диагонали образуют со стороной AB углы 50 и
60. Какие углы образуют диагонали со стороной CD?
Задача 5:
Задача 6:
Задача 7:
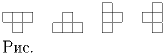
Дана шахматная доска 1990 × 1990. Разрешается
одновременно заменить цвет (белый на чёрный, а чёрный на белый) у
любых четырёх клеток, образующих фигуры такого вида, как показано на
рисунке . Можно ли в результате нескольких таких операций изменить
цвет всех клеток шахматной доски на противоположный?
Задача 8:
Дан треугольник ABC. Точка K — середина стороны AB, а
точки L и M выбраны произвольно соответственно на сторонах BC и
AC. Доказать, что S
∆ KLM < S
∆ BKL + S
∆ AKM.


