 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1991, Винница >> 10 класс | Показать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1991, Винница. 10 класс |
|
|
Задача 2: Пусть f(x) — многочлен с целыми коэффициентами и f(1991) = 1. а) Доказать, что не существует таких целых чисел m, n и k, что f(m) = f(n) = f(k) = 0. б) Остается ли утверждение а) правильным, если ограничиться лишь двумя целыми числами m, n?
Задача 3: Доказать, что из произвольного равнобедренного треугольника, площадь которого равна S, можно вырезать три равных треугольника, площадь каждого из которых больше
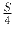 .
.Задача 4: В пространстве даны три прямые a, b и c. На прямой a взята точка M0. Из точки M0 провели перпендикуляр к прямой b до пересечения с нею в точке M1. Из точки M1 провели перпендикуляр к прямой c до пересечения с нею в точке M2. Из точки M2 провели перпендикуляр снова к прямой a до пересечения с нею в точке M3 и т.д. Доказать, что если M6 = M0, то и M3 = M0.
Задача 5: Все числа
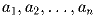 больше 1 и для любого k, 1 ≤ k ≤ n – 1, выполняется неравенство |ak + 1 – ak| < 1. Доказать,
что
больше 1 и для любого k, 1 ≤ k ≤ n – 1, выполняется неравенство |ak + 1 – ak| < 1. Доказать,
что 
Задача 6: Из n³ одинаковых кубиков сложен куб с ребром n, в котором произвольно отмечены более 1,5n² одинаковых кубиков. Доказать, что найдётся прямоугольный треугольник, вершинами которого являются центры отмеченных кубиков, каждый катет которого параллелен некоторому ребру куба.
Задача 7: Делегаты съезда должны избрать комиссию. Каждый делегат избрал 10 лиц из списка кандидатур. Комиссия устраивает делегата, если в ней есть хотя бы одно избранное им лицо. выяснилось, что для любых 6 делегатов можно найти устраивающую их комиссию из двух лиц. Доказать, что можно избрать комиссию из 10 лиц, устраивающую всех делегатов.
Задача 8: На плоскости α выбрали произвольным образом точку A и окружность γ . От каждой точки B окружности отложили перпендикуляр к плоскости α , длина которого равна квадрату длины отрезка AB (все перпендикуляры отложены в одну сторону от плоскости α ). Доказать, что концы этих перпендикуляров лежат в одной плоскости.
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1991, Винница >> 10 класс | Показать решения |