 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1991, Винница >> 9 класс | Показать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1991, Винница. 9 класс |
|
|
Задача 2: Решить уравнение [x]x + x = 2x + 10, где [x] и x — соответственно целая и дробная части числа x.
Задача 3: На сторонах AB, BC, CA треугольника ABC взяты точки E, F, G так, что AE:AB = x, BF:BC = y, CG:CA = z. Площадь треугольника ABC равна S. Вычислить площадь треугольника EFG.
Задача 4: На плоскости дана точка O и два одинаковых квадрата F1 и F2 площади S. Фигура F образована всеми такими точками B, что вектор
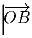 можно записать в виде
можно записать в виде 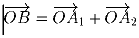 , где точка A1 лежит в квадрате F1, а точка A2
— в квадрате F2. Найти наименьшее и наибольшее возможные
значения площади фигуры F в зависимости от взаимного расположения
квадратов F1 и F2.
, где точка A1 лежит в квадрате F1, а точка A2
— в квадрате F2. Найти наименьшее и наибольшее возможные
значения площади фигуры F в зависимости от взаимного расположения
квадратов F1 и F2.Задача 5: Даны три различных положительных числа. Доказать, что одно из них можно обозначить через a, другое — через b и третье — через c так, чтобы выполнялось неравенство
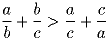
Задача 6: На сторонах треугольника ABC вне его построены параллелограммы APQC, BMNC и AEFB так, что четырёхугольник AECK также является параллелограммом (K — точка пересечения прямых PQ и MN). Доказать, что площадь параллелограмма AEFB равна сумме площадей параллелограммов APQC и BMNC.
Задача 7: В классе учится n учеников, и каждый день двое из них дежурят. На некоторый период времени нужно так составить график дежурств, чтобы для любых двух учеников нашёлся день, когда один из них дежурит, а другой — нет. Какое наименьшее количество дней может охватывать такой график?
Задача 8: Известно, что многочлен 2x³ – 60x² + ax, где a — целое число, при некоторых трёх натуральных последовательных значениях аргумента x принимает три последовательных натуральных значения. Найти эти значения многочлена.
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1991, Винница >> 9 класс | Показать решения |