 |
 |
|
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1992, Чернигов >> 11 класс | Показать решения |
|
|
| Украинские соревнования. Всеукраинская олимпиада школьников. 1992, Чернигов. 11 класс |
|
|
Задача 2: Через точку K, взятую на стороне AB треугольника ABC, проведены прямая параллельно стороне AC до пересечения со стороной BC в точке L и прямая параллельно BC до пересечения с AC в точке M. При каком положении точки K площадь треугольника KLM будет наибольшей? Чему равна эта площадь, если площадь треугольника ABC равна S0?
Задача 3: В каждой вершине правильного 1992-угольника записано положительное число, причём каждое из чисел равно или среднему арифметическому, или среднему геометрическому двух чисел, записанных в соседних вершинах. Известно, что среди записанных чисел есть 26. Найти остальные записанные числа.
Задача 4: Доказать, что
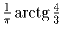 —
иррациональное число.
—
иррациональное число.Задача 5: Доказать, что при a > b > c выполнено неравенство
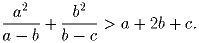
Задача 6: Пусть AA1, BB1, CC1 — высоты треугольника ABC. Доказать, что равенство
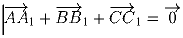 выполняется тогда и только тогда, когда треугольник ABC
правильный.
выполняется тогда и только тогда, когда треугольник ABC
правильный.Задача 7: Основанием пирамиды SABCD служит прямоугольник ABCD. Боковое ребро SA перпендикулярно плоскости основания. Плоскость, проходящая через вершину A перпендикулярно ребру SC, пересекает боковые рёбра SB, SC и SD в точках B1, C1 и D1 соответственно. Доказать, что вокруг многогранника ABCDB1C1D1 можно описать сферу.
Задача 8:
| Задачная база >> Украинские соревнования >> Всеукраинская олимпиада школьников >> 1992, Чернигов >> 11 класс | Показать решения |