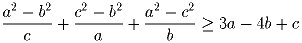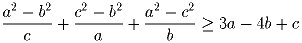Задача 1:
Доказать, что если для натуральных чисел m и n справедливо
равенство 2n = m² + 1, то число n можно представить в виде суммы двух
квадратов целых чисел.
Задача 2:
Четырёхугольник ABCD вписан в окружность, а центр O этой
окружности лежит внутри четырёхугольника. Известно, что ∠ AOB + ∠ COD = 180. Доказать, что сумма длин перпендикуляров, опущенных из точки
O на стороны четырёхугольника, равна половине его периметра.
Задача 3:
На каждой грани непрозрачного куба написано некоторое натуральное
число. Если несколько граней куба (одну, две или три) можно увидеть
одновременно, то выписываем сумма чисел, написанных на этих гранях. Какое
наибольшее количество различных чисел можно выписать?
Задача 4:
Известно, что значение трёхчлена ax² + bx + c для
любого целого числа x также является целым числом. Обязательно ли:
а) хотя бы один из коэффициентов a, b, c является целым числом;
б) все коэффициенты a, b и c — целые?
Задача 5:
На плоскости даны точки A, B, C и D, причём известно, что из
точек A, C и D ближе всего к B лежит точка A, а из точек A, B и
C ближе всего к D лежит точка C. Доказать, что отрезки AB и CD не
пересекаются.
Задача 6:
Доказать, что для любых положительных чисел a, b, c,
удовлетворяющих условию a ≥ b ≥ c, выполняется неравенство