 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> V, 1994 >> Турнир матбоёв >> Высшая лига >> 3-й тур | Показать решения |
|
|
| V Всероссийский фестиваль юных математиков. Михайловский. 1994. Турнир матбоёв. Высшая лига. 3-й тур |
|
|
Задача 2: Дан параллелограмм ABCD ( ∠ BAD – острый). Биссектриса угла BAD пересекает сторону CD в точке L, а прямую BC – в точке K. Пусть O – центр окружности, описанной около треугольника LCK. Докажите, что точки D, B, C и O лежат на одной окружности.
Задача 3: Дана функция f(x) = x² – 3|x| + 4. Найдите все множества A, состоящие из конечного числа элементов и обладающие следующим свойством: для любого числа x, принадлежащего множеству A, число f(x) также принадлежит множеству A.
Задача 4: Можно ли разбить множество натуральных чисел на три непустых попарно непересекающихся множества так, чтобы для каждой пары чисел x и y, взятых из любых двух разных множеств, число xy + x + y принадлежало бы третьему множеству?
Задача 5: Даны последовательности an и dn: an = 100 + n², dn – наибольший общий делитель чисел an и an + 1. Какое наибольшее значение может принимать dn?
Задача 6: Найдите все функции f(x):R → R, которые для любых x и y удовлетворяют равенству f(x² + y) = f(x) + f(y).
Задача 7: Даны 27 (не обязательно различных) положительных чисел
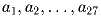 . Рассматриваются тройки индексов (k,m,n) такие, что
ak < am, ak + am = an. Каково наибольшее возможное количество
таких троек?
. Рассматриваются тройки индексов (k,m,n) такие, что
ak < am, ak + am = an. Каково наибольшее возможное количество
таких троек?Задача 8: Сфера с центром O касается всех ребер тетраэдра. Четыре сферы с центрами в вершинах тетраэдра попарно касаются друг друга внешним образом, а также касаются некоторой сферы с центром O. Докажите, что тетраэдр является правильным.
Задача 9: Пусть α (x) и β (x) – многочлены, степень каждого из которых больше единицы, ρ (x) = α ( β (x)). Пусть многочлен ρ (x) – четен. Докажите, что многочлен β (x) – β (0) – четен или нечетен.
Задача 10: В стране 22 аэродрома, и каждый связан авиарейсами с тремя другими. Докажите, что есть такая пара аэродромов A и B, для которой любой перелет из A в B требует не менее трех пересадок.
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> V, 1994 >> Турнир матбоёв >> Высшая лига >> 3-й тур | Показать решения |