 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> VI, 1995 >> Турнир матбоёв >> Финал | Показать решения |
|
|
| VI Всероссийский фестиваль юных математиков. Анапа. 1995. Турнир матбоёв. Финал |
|
|
Задача 2: Упростите выражение:
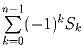 , где
, где
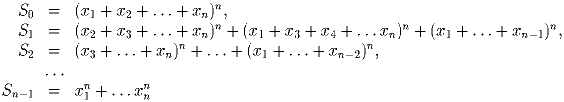
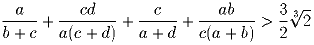
Задача 5: С натуральным числом можно производить следующую операцию: умножить его на любое однозначное число и из полученного произведения вычеркнуть все единицы. Найдите все натуральные n, которые после нескольких применений указанной операции могут быть переведены в число 2.
Задача 6: Рассмотрим последовательности (an) , удовлетворяющие следующим условиям: a1 = 2, a2 = 3, an + 2 ∈ 2an;3an + 1 – 2an, n ∈ N. Докажите, что ни одна из этих последовательностей не содержит ни одного шестизначного числа, начинающегося с 8 или 9.
Задача 7: Найдите все положительные рациональные числа x, y, z такие, что числа x + y + z,
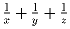 , xyz – целые.
, xyz – целые.Задача 8: В выпуклом шестиграннике все грани – четырехугольники, а семь его вершин лежат на одной сфере. Докажите, что и восьмая вершина лежит на этой сфере.
Задача 9: На плоскости расположены 5 точек общего положения, причем площадь любого треугольника с вершинами в этих точках больше 3. Докажите, что площадь хотя бы одного из этих треугольников больше 4.
Задача 10: В данный остроугольный треугольник впишите равносторонний треугольник наименьшей площади.
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> VI, 1995 >> Турнир матбоёв >> Финал | Показать решения |