Задача 1:
Задача 2:
Длины сторон треугольника – факториалы натуральных чисел.
Докажите, что этот треугольник равнобедренный.
Задача 3:
Докажите, что при всех действительных x выполнено неравенство:
x² + x cos x + x² sin x + 1/2 > 0.
Задача 4:
На стороне AB равностороннего треугольника ABC взята точка
A
1. Точка A
2 – проекция точки A
1 на сторону BC, точка
A
3 – проекция A
2 на сторону C
A, точка A
4 – проекция
A
3 на сторону AB, и т.д. Найдите все положения точки A
1, при
которых A
94 = A
1.
Задача 5:
Дана окружность с центром S. Хорда AB не проходит через S. C –
внутренняя точка AB. Окружность, описанная вокруг треугольника ASC,
пересекает вторично данную окружность в точке D. Докажите, что CD = CB.
Задача 6:
Можно ли расставить 100 целых чисел по кругу так, чтобы для
любого числа n от 1 до 100 среди расставленных чисел нашлись бы три
последовательных числа, сумма которых равна n?
Задача 7:
Каждой точке координатной плоскости поставлено в соответствие
некоторое число. Известно, что для любого квадрата со сторонами,
параллельными осям координат, сумма чисел, соответствующих его
вершинам равна нулю. Докажите, что все числа равны нулю.
Задача 8:
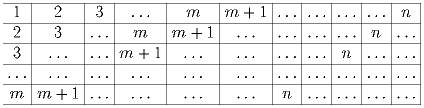
В клетках прямоугольной таблицы m × n записаны числа так,
как показано на рисунке. Найдите сумму всех чисел в таблице.
Задача 9:
Рассмотрим набор из 1994 действительных чисел, не больших 100,
удовлетворяющий условию: как бы ни разбивать эти числа на две
непустые группы, сумма чисел хотя бы в одной из групп будет не больше
100. Найдите наибольшую возможную сумму чисел в таком наборе.
Задача 10:
Пятнадцать спичек лежат в ряд. Спички собираются в группы,
состоящие из одной или более спичек. За один ход можно переместить
любую отдельно лежащую спичку в группу, перескакивая ровно через 3
спички, лежащие отдельно или в группах. Соберите спички в пять групп
по три в каждой.


