Задача 1:
Функция f(x):R → R такова, что f(f(x)) = e
– x. Докажите, что
она имеет бесконечное число точек разрыва.
Задача 2:
При каких целых неотрицательных n набор из n единичных
квадратиков можно дополнить несколькими (не менее одной) фигурками
вида

так, что из всего полученного набора можно
будет составить прямоугольник?
Задача 3:
В остроугольном треугольнике одна из вершин, центры вписанной и
описанной окружностей, а также ортоцентр лежат на одной окружности.
Докажите, что один из углов треугольника равен 60.
Задача 4:
Сумма положительных чисел a, b и c меньше π , и эти числа
являются длинами сторон некоторого треугольника. Докажите, что синусы
этих углов также являются длинами сторон некоторого треугольника.
Задача 5:
Найдите все функции f(x) такие, что f(0) = 0 и |f′(x)| ≤ 1995|f(x)|
при всех вещественных x.
Задача 6:
Таблица 1000 × 1000 заполнена числами 0 и 1 так, что сумма
чисел в любом квадрате 3 × 3 равна нулю. Какое наибольшее
значение может принимать сумма всех чисел таблицы?
Задача 7:
Прямая, проходящая через центр вписанной в треугольник ABC
окружности, пересекает стороны AC и BC в точках E и F.
Докажите, что
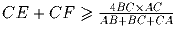
.
Задача 8:
Найдите все многочлены P(x) такие, что для всех действительных
x P(x²) + P(x³) = P(x³ + 1).
Задача 9:
Пусть A – бесконечное множество натуральных чисел, такое, что
любой его элемент является произведением не более чем 1995 простых
чисел. Докажите, что можно найти натуральное число n и бесконечное
множество BA такие, что наибольший общий делитель любых двух
различных чисел из B равен n.
Задача 10:
Последовательность (x
n) такова, что x
0 = 2, x
1 = x
2 = a,
x
n + 2 = x
n + 1x
n – x
n – 1
для всех натуральных n. Известно, что a – рационально, а
последовательность (x
n) периодична. Какой может быть длина ее
периода?


 так, что из всего полученного набора можно
будет составить прямоугольник?
так, что из всего полученного набора можно
будет составить прямоугольник?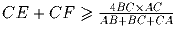 .
.