 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> I, 1990 >> Турнир матбоёв >> 2-й тур | Убрать решения |
|
|
| I Всероссийский фестиваль юных математиков. Краснодар. 1990. Турнир матбоёв. 2-й тур |
|
|
Решение: Ответ:
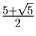 .
Задача 2:
Внутри квадрата со стороной 2 расположено 7 многоугольников
площади не менее 1 каждый. Докажите, что существует два
многоугольника, площадь пересечения которых не менее 1/7.
.
Задача 2:
Внутри квадрата со стороной 2 расположено 7 многоугольников
площади не менее 1 каждый. Докажите, что существует два
многоугольника, площадь пересечения которых не менее 1/7.Задача 3: Сто сумасшедших красят доску 100 × 100 в 100 цветов, соблюдая единственное правило: в одной строке и в одном столбце не может быть двух клеток, раскрашенных одинаково. Могут ли сумасшедшие правильно раскрасить доску, если уже раскрашено 100 клеток?
Решение: Нет, не всегда. Раскрасим первые 99 клеток первой строки в первые 99 цветов, а последнюю клетку второй строки – в оставшийся 100-й цвет. Тогда последнюю клетку первой строки раскрасить уже не удастся. Задача 4: Первый член последовательности ak равен 1, остальные вычисляются по правилу:
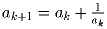 . Докажите,
что a100 > 14.
. Докажите,
что a100 > 14.Решение: Заметьте, что
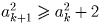 .
Задача 5:
Что больше:
.
Задача 5:
Что больше: 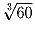 или
или 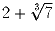 ?
?Решение: Первое число больше. Задача 6: На плоскости отмечено несколько точек, не все на одной прямой. В каждой точке записано число, причем сумма чисел в точках, лежащих на одной прямой равна 0. Докажите, что все числа равны 0.
Задача 7: Единичный квадрат разбит двумя способами на n равновеликих многоугольников. Докажите, что можно выбрать n точек так, что в каждой из полученных 2n частей окажется по одной точке.
Задача 8: Пусть n – натуральное число, а d – натуральный делитель числа 2n². Докажите, что n² + d не является квадратом.
Решение: Пусть 2n² = dq. Предположим противное, т.е. n² + d = k². Тогда легко получить, что n²(2 + q) = k²q. Если q нечетно, то q и q + 2 взаимно просты, а значит, являются полными квадратами, чего не может быть. Если же q четно, то взаимно просты q/2 и 1 + q/2, а значит, являются полными квадратами, чего также не может быть. Задача 9: В городе Метрополисе каждая линия метро соединяет две станции. При закрытии любых девяти с каждой станции можно добраться до каждой. Докажите, что 10 путешественников могут проехать от площади Чернова до площади Белова попарно непересекающимися маршрутами (отсутствуют пересечения на станциях).
Задача 10: Некоторое множество целых чисел, среди которых есть как положительные, так и отрицательные, вместе с каждыми своими элементами a и b содержит 2a и a + b. Докажите, что это множество содержит разность любых двух своих элементов.
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> I, 1990 >> Турнир матбоёв >> 2-й тур | Убрать решения |