 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> I, 1990 >> Турнир матбоёв >> 3-й тур | Убрать решения |
|
|
| I Всероссийский фестиваль юных математиков. Краснодар. 1990. Турнир матбоёв. 3-й тур |
|
|
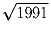 . От него
отрезают квадрат, а с оставшимся прямоугольником делают ту же
процедуру. Доказать, что последовательность отношений больших сторон
к меньшим построенных прямоугольников периодична начиная с некоторого
номера.
. От него
отрезают квадрат, а с оставшимся прямоугольником делают ту же
процедуру. Доказать, что последовательность отношений больших сторон
к меньшим построенных прямоугольников периодична начиная с некоторого
номера.Задача 2: Луч прожектора на маленьком острове имеет в тумане длину 1 км (отрезок длиной 1 км) и вращается со скоростью 1 об/мин. Катер хочет высадить десант на остров. Какова должна быть минимальная скорость катера, чтоб он мог это сделать?
Задача 3: Пусть a1, b1, c1, a2, b2, c2 – такие вещественные числа, что при любых целых x и y по крайней мере одно из чисел a1x + b1y + c1 и a2x + b2y + c2 – четное. Докажите, что по крайней мере в одной из троек коэффициентов a1, b1, c1 и a2, b2, c2 все числа – целые.
Решение: Подставим x = 0, y = 0. Получим, что либо c1, либо c2 – целое. Подставим x = 1, y = 0 и x = 2, y = 0. Получим, что либо a1 и c1, либо a2 и c2 – целые. Аналогично получаем, что либо b1 и c1, либо b2 и c2 – целые. Далее, подставив x = y = 1, легко получаем требуемое утверждение. Задача 4: Определим функцию G(n), полагая G(n) = n/2 для четного n и G(n) = 3n – 1 для нечетного n. Конечно или бесконечно множество чисел периода 10? (Число n имеет период k, если G(G...G(n)...) = n, где функция G применяется k раз).
Решение: Понятно, что после «раскрытия скобок" у нас получится уравнение вида
 , которое имеет ровно одно
решение. Осталось заметить, что различных вариантов троек (a,b,c) –
конечное число (не более чем 2¹º), а значит, и чисел,
удовлетворяющих условию, конечное число.
Задача 5:
Даны правильный тетраэдр и шар. Тетраэдр разрешается отражать от
любой его грани. Можно ли добиться, что центр тетраэдра окажется
внутри шара?
, которое имеет ровно одно
решение. Осталось заметить, что различных вариантов троек (a,b,c) –
конечное число (не более чем 2¹º), а значит, и чисел,
удовлетворяющих условию, конечное число.
Задача 5:
Даны правильный тетраэдр и шар. Тетраэдр разрешается отражать от
любой его грани. Можно ли добиться, что центр тетраэдра окажется
внутри шара?Задача 6: В стране Метрополии каждый город связан с каждым дорогой. Злой волшебник установил на всех дорогах одностороннее движение. Тем не менее, оказалось, что из любого города можно добраться до любого другого. Доказать, что существует замкнутый путь, проходящий через все города Метрополии один раз.
Задача 7: Вещественные положительные числа a, b, x, y удовлетворяют неравенствам a5 + b5 ≤ 1, x5 + y5 ≤ 1. Докажите, что a²x³ + b²y³ ≤ 1.
Задача 8: Пусть X, Y, Z – центры квадратов, построенных во внешнюю сторону на сторонах BC, CA, AB треугольника ABC. Докажите, что отрезок AX равен и перпендикулярен к YZ.
Задача 9: Найдите все многочлены f(x) с целыми неотрицательными коэффициентами, принимающие простые значения при простом значении аргумента.
Задача 10: Рассмотрим все пирамиды, в основании которых лежит данный остроугольный треугольник ABC, а боковыми гранями служат остроугольные треугольники. Найдите геометрическое место оснований высот пирамиды, опущенных на плоскость треугольника ABC.
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> I, 1990 >> Турнир матбоёв >> 3-й тур | Убрать решения |