Задача 1: Можно ли расположить в пространстве систему окружностей так, чтобы через каждую точку проходила ровно одна окружность?

Задача 2: Существует ли система отрезков единичной длины на прямой, такая, что:

1) отрезки не пересекаются;

2) любая бесконечная арифметическая прогрессия содержит точку системы.

Решение: Рассмотрим следующую систему отрезков: [0;1], [2;3], [3½;4½], 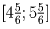 – т.е. длины всех отрезков равны 1, а расстояния между концами соседних отрезков равны 1, 1/2, 1/3, 1/4, 1/5, …Предположим, что какая-то арифметическая прогрессия не содержит точек системы. Заметим, что начиная с некоторого шага между двумя соседними точками прогрессии будет лежать одинаковое число наших отрезков – а именно 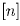, где n – разность прогрессии. Рассмотрим теперь некоторый шаг прогрессии, который перепрыгнул через наши отрезки с номерами k, k + 1, …, k + [n] – 1. Нетрудно убедиться, что тогда число n должно принадлежать интервалу

Это же условие должно выполняться и для больших значений k. Осталось только заметить, что для достаточно больших k соответствующий интервал не будет пересекаться с только что выписанным интервалом. Полученное противоречие показывает, что наша система отрезков удовлетворяет условию.

Задача 3: Два многочлена P и Q имеют одинаковый набор корней, то же верно для P′ и Q′ . Докажите, что P и Q пропорциональны степеням некоторого многочлена R.

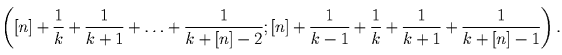
Задача 4: На шахматной доске отмечены центры всех 64 клеток. Можно ли 13 прямыми разбить на части доску так, чтобы в любой из них было не более одного центра?

Решение: Рассмотрим 28 клеток по периметру доски. Соединим центры соседних из этих 28 клеток отрезками. Так как каждая прямая пересекает не более двух таких отрезков, то какой-то отрезок окажется не пересеченным, а значит соответствующие две клетки окажутся в одной части.

Задача 5: Пусть x₁,x₂, … ,x_n > 0, k₁ < k₂. Докажите неравенство:

где сумма берется по всем различным наборам из k₁ и k₂ элементов соответственно.

Задача 6: Дан набор из P чисел, каждое равно  + 1 или  – 1. За одну операцию можно изменить знак нескольких стоящих подряд чисел. За какое минимальное число таких операций можно прийти к набору из одних  + 1?

Задача 7: Рассмотрим последовательность a_i: a_n – первая цифра числа 2ⁿ в десятичной записи. Докажите, что существует такое k, что в каждом куске длины k последовательности встретится кусок 2481361251.

Задача 8: Найдите такое N, что число 5^N имеет 1000 подряд идущих нулей.

Задача 9: Даны две окружности, одна внутри другой. Берется точка P₀ внешней окружности и проводится касательная к внутренней. P₁ – вторая точка пересечения касательной с внешней окружностью. Далее так строятся точки P₂, P₃, …, P_n. Докажите, что если для некоторой начальной точки произошло зацикливание через n шагов, то это верно при любом начальном выборе точки P.

Задача 10: Замкнутая ломаная проходит по всем граням куба со стороной 1. Докажите, что ее длина не меньше .

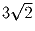Решение: Указание: рассмотрите развертку куба.