 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> II, 1991 >> Турнир матбоёв >> 1-й тур | Убрать решения |
|
|
| II Всероссийский фестиваль юных математиков. Краснодар. 1991. Турнир матбоёв. 1-й тур |
|
|
Решение: Ответ: m = 1,2,4. Задача 2: У Пети циркуль с раствором ножек 10 см и линейка без делений длиной 20 см. Сможет ли он соединить отрезком две точки на расстоянии 1 метр?
Задача 3: В городе Плюралийске 30 районов, 30 параллельных улиц, пересекающих эти районы и 30 политических партий. Каждая партия хочет иметь по одному райкому в каждом районе и на каждой улице. Мэр города, идя навстречу политикам, уже выделил 899 зданий под райкомы. Всегда ли он сможет выделить последнее здание, удовлетворив все партии?
Решение: Да, всегда. Задача 4: На плоскости лежат правильный восьмиугольник и круг. Восьмиугольник можно поворачивать вокруг центра и симметрично отражать относительно любой его стороны. Докажите, что за конечное число таких операций можно добиться, чтобы центр восьмиугольника попал в данный круг.
Решение: Обозначим через M множество точек плоскости, в которые можно за конечное число шагов перенести центр O восьмиугольника. Ясно, что вместе с центром O множеству M принадлежат все точки, симметричные относительно середин сторон восьмиугольника. Поворачивая восьмиугольник вокруг центра, можно считать, сто середины сторон заполняют окружность, вписанную в него. Значит, M содержит окружность с тем же центром удвоенного радиуса. Используя любую точку этой окружности в качестве центра, включаем в M точки всех окружностей этого же радиуса. Их объединение заполнит весь круг с центром O вдвое большего радиуса. Понятно, что таким образом можно включить в M любую точку плоскости.
Задача 5: Четные натуральные числа a и b получаются друг из друга некоторой перестановкой цифр. Докажите, что суммы цифр чисел a/2 и b/2 равны.
Решение: Пусть S(x) и N(x) – соответственно сумма цифр числа x и количество цифр в x, больших 4. Понятно, что S(x) = 2S(x/2) – 9N(x/2). Осталось только заметить, что N(x/2) равно количеству нечетных цифр числа x.
Задача 6: В прямоугольном параллелепипеде из одной вершины проведено 3 диагонали граней. Докажите, что сумма углов между этими диагоналями равна 1800.
Решение: Соединив попарно концы трех проведенных диагоналей, получим вписанный в параллелепипед тетраэдр с равными гранями. Сумма указанных углов равна сумме углов любой грани этого тетраэдра.
Задача 7: На окружности длины 1 заданы две конечные системы дуг. Общая длина дуг каждой из систем 1/2. Докажите, что одну из систем можно повернуть вокруг центра окружности так, что общая длина ее пересечения с дугами второй системы будет не меньше 1/4.
Задача 8: Докажите для каждого натурального n неравенство:
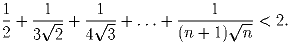
Решение: Указание. Докажите по индукции более сильное неравенство:
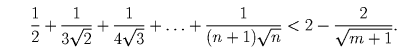
Решение:
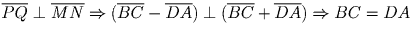 .
Задача 10:
Докажите, что для любого натурального n > 80 куб можно
разрезать на n кубов (среди которых могут быть и одинаковые).
.
Задача 10:
Докажите, что для любого натурального n > 80 куб можно
разрезать на n кубов (среди которых могут быть и одинаковые).Решение: Заметим, что если куб можно разбить на n кубиков, то его можно разбить и на n + 7 кубиков. Осталось лишь найти разбиения для семи конкретных значений n, меньших 80, и дающих разные остатки от деления на 7. Такими могут быть, например, следующие: 8, 27, 38, 39, 58, 75, 77.
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> II, 1991 >> Турнир матбоёв >> 1-й тур | Убрать решения |