Задача 1: Плоскость раскрасили в 5 цветов. Докажите, что существует 2 точки одного цвета, расстояние между которыми отлично от 1 не более чем на 0,001.

Задача 2: При каком условии бесконечная арифметическая прогрессия a, a + d, …, a + nd,  …  содержит в себе подпоследовательность, являющуюся бесконечной геометрической прогрессией?

Решение: Необходимым и достаточным условием является рациональность отношения a/d.

Задача 3: На каждой стороне параллелограмма взято по точке. Площадь четырехугольника с вершинами в этих точках равна половине площади параллелограмма. Докажите, что какая-то диагональ четырехугольника параллельна одной из сторон параллелограмма.

Решение: Пусть ABCD – этот параллелограмм, X, Y, Z, T – точки соответственно на AB, BC, CD, DA. Допустим, что XZ не параллельно AD. Будем двигать точку T по AD. При этом площадь четырехугольника XYZT будем изменяться монотонно, и окажется равной половине площади параллелограмма только когда YT\|AB.

Задача 4: В концах отрезка пишутся две единицы. Посередине между ними пишется их сумма – 2. Затем посередине между каждыми соседними пишут их сумму, ... и.т.д. – 1991 раз. Сколько раз будет написано число 1991?

Решение: Будем говорить, что пара (a,b) входит в написанный ряд, если между числами a и b нет других чисел. Нетрудно убедиться, что пара (a,b) входит в ряд на каком-то шаге тогда и только тогда, когда числа a и b взаимно просты. Значит, ответ – количество чисел, взаимно простых с 1991 и меньших 1991, т.е. 1800.

Задача 5: Докажите, что к конечному множеству точек на плоскости, обладающему тем свойством, что любые три точки этого множества являются вершинами невырожденного тупоугольного треугольника, всегда можно добавить одну точку так, что это свойство сохранится.

Решение: Нарисуем для каждой пары отмеченных точек «запретную" полосу. Понятно, что все эти полосы не покроют плоскость, и можно добавить еще точку.

Задача 6: Докажите, что если сумма двух натуральных чисел равна 19910, то их произведение не делится на 19910.

Решение: Разложите 19910 на простые сомножители, и докажите, что оба числа должны делиться на каждый из этих сомножителей, чего не может быть.

Задача 7: Функция f(x) определена на множестве 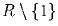и удовлетворяет тождеству f(x) + 2f((x – 2)/(x – 1)) = x. Найти все такие функции f(x).

Решение: Подставьте вместо x выражение 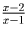. Ответ: .

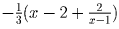Задача 8: В углу шахматной доски размером N × N клеток (N > 4), стоит фигура. Первый игрок может ходить ею 2 раза подряд как обычным конем, а второй – один раз как конем с удлиненным ходом (на три клетки в одном направлении и на одну в перпендикулярном). Так они ходят по очереди. Первый игрок стремится поставить фигуру в противоположный угол, а второй – ему помешать. Кто из них выиграет?

Решение: Выигрывает первый игрок. Он может действовать так, чтобы каждой своей парой ходов возвращать фигуру на главную диагональ, продвигая ее ближе к нужному углу.

Задача 9: Вычислите сумму:

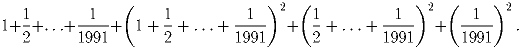
Решение: По индукции доказывается равенство:

Задача 10: На каждом ребре выпуклого многогранника поставлена стрелка так, что в каждую вершину многогранника входит и из каждой вершины выходит хотя бы одна стрелка. Докажите, что существуют по крайней мере 2 грани многогранника, которые можно обойти по периметру, двигаясь по направлению стрелок.

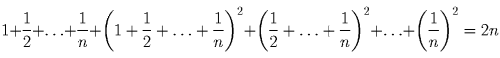
Решение: Начав с любой вершины и двигаясь по стрелкам, находим цикл, разбивающий поверхность на две области. Взяв внутри области ребро, не входящее в границу, построим новый цикл, содержащий меньше граней, чем область. Продолжая процесс, получим цикл, содержащий одну грань.