 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> II, 1991 >> Турнир матбоёв >> 3-й тур | Убрать решения |
|
|
| II Всероссийский фестиваль юных математиков. Краснодар. 1991. Турнир матбоёв. 3-й тур |
|
|
Задача 2: Бумажный квадрат складывается пополам по некоторой прямой l, проходящей через его центр в невыпуклый 9-угольник. Для какой прямой l этот 9-угольник имеет максимальную площадь?
Решение: Если отразить полученный 9-угольник относительно прямой l, то получится фигура, являющаяся объединением двух квадратов, один из которых повернут относительно центра на угол 2 α , где α – угол между l и горизонтальной стороной исходного квадрата. Максимальная площадь будет при 2 α = 45. Задача 3: Дано слово длины 2n². Докажите, что либо в нем можно указать n различных подслов длины n² каждое, либо какая-то комбинация букв повторяется n раз подряд.
Решение: Воспользуйтесь методом «от противного". Задача 4: Докажите, что уравнение a² + b² + c² – 3abc = 6 имеет бесконечно много решений в целых числах.
Задача 5: Дано преобразование плоскости, которое сохраняет все целочисленные расстояния между точками (т.е. если расстояние между точками равно целому числу, то расстояние между их образами равно тому же числу). Докажите, что оно сохраняет расстояния между любыми двумя точками.
Задача 6: Докажите, что если a1a2 … an = Pn, то справедливо неравенство:
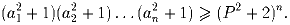
Решение: Пусть все ai неотрицательны. Докажите, что при сближении двух ai и aj с постоянным произведением левая часть неравенства уменьшается (метод Штурма). Т.к. при равенстве всех ai между собой неравенство выполняется (и обращается в равенство), то неравенство верно всегда. Задача 7: Дано бесконечное множество многочленов от 10 переменных. Докажите, что из него можно выбрать такое конечное число многочленов P1, P2, …, Pn, что всякий многочлен P этого семейства представим в виде P1Q1 + P2Q2 + … + PnQn, где Q1, …Qn – некоторые многочлены (не обязательно из этого семейства).
Задача 8: В пространстве дано выпуклое тело. Докажите, что на его поверхности можно выбрать такие 4 точки, что для каждой из них плоскость, касающаяся тела в этой точке, параллельна плоскости, проходящей через 3 другие точки.
Задача 9: Для каких n существуют такие 2 прогрессии – арифметическая a1, a2, … и геометрическая b1, b2, … что a1 < b1 < a2 < b2 < a3 < … < an < bn < an + 1?
Задача 10: Точка O – середина оси прямого кругового цилиндра. A и B – диаметрально противоположные точки окружности нижнего основания цилиндра. C – некоторая точка окружности верхнего основания, не лежащая в плоскости OAB. Докажите, что сумма двугранных углов трехгранного угла OABC (с вершиной O) равна 2 π .
Решение: Возьмем точку D, диаметрально противоположную C, и рассмотрим тетраэдр ABCD. Трехгранные углы OABC, OACD, OBCD, OABD равны, т.к. имеют равные плоские углы. Каждые три из этих трехгранных углов имеют общее ребро. Сумма трех двугранных углов при этом ребре равна 2 π . Тогда сумма всех двугранных углов при ребрах OA, OB, OC, OD равна 8 π . Из равенства всех трехгранных углов получаем утверждение задачи.
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> II, 1991 >> Турнир матбоёв >> 3-й тур | Убрать решения |