 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> III, 1992 >> Турнир матбоёв >> 1-й тур | Убрать решения |
|
|
| III Всероссийский фестиваль юных математиков. Краснодар. 1992. Турнир матбоёв. 1-й тур |
|
|
Решение: Т.к. 61(m + n) = 77m, то m + n делится на 77. Задача 2: Обозначим через a(n) число способов, которыми данное натуральное число n можно представить в виде суммы нескольких (быть может, одного) натуральных слагаемых, больших единицы, с учетом их порядка. Докажите для каждого n тождество: a(2) + a(4) + ... + a(2n) = a(2n + 1).
Решение: Докажите по индукции, что a(n + 2) = a(n + 1) + a(n). Задача 3: Найдите все многочлены P(x) такие, что для каждого x выполняется равенство: xP(x – 1) = (x – 10)P(x).
Решение: Ответ: C(x – 9)(x – 8) … (x – 1)x. Задача 4: Пусть an – число нулей, которыми оканчивается число n! = 1 × 2 × … × n в десятичной записи. Докажите, что существует
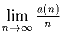 и
вычислите его.
Решение:
Понятно, что an – это количество пятерок в разложении n!
на простые сомножители. Записав известную формулу для этой величины
(сумма целых частей), и оценив целые части, получим геометрическую
прогрессию, сумма которой равна ¼.
и
вычислите его.
Решение:
Понятно, что an – это количество пятерок в разложении n!
на простые сомножители. Записав известную формулу для этой величины
(сумма целых частей), и оценив целые части, получим геометрическую
прогрессию, сумма которой равна ¼.Задача 5: Докажите, что алгебраическое уравнение xn + a1xn – 1 + an – 1x + an = 0, среди коэффициентов которого встречаются только числа ± 1 и 0, не имеет действительных корней, модуль которых превышает 2.
Решение: Если |x0| > 2 и |x0| – корень уравнения, то |x0|n ≤ |x0|n – 1 + … |x0| + 1 < |x0|n – 1 Задача 6: Центры трех попарно касающихся внешним образом окружностей лежат в вершинах прямоугольного треугольника. Найдите радиус четвертой окружности, касающейся трех данных и содержащей их внутри себя, если периметр треугольника равен p.
Решение: Отразим вершину прямого угла данного треугольника симметрично относительно середины его гипотенузы. Полученная точка является центром окружности, касающейся трех данных нужным образом. Радиус четвертой окружности равен сумме радиусов первых трех, т.е. полупериметру. Задача 7: На плоскость положили четыре прямых круговых конуса с общей вершиной и одинаковой образующей (но, вообще говоря, с различными радиусами основания) так, что каждый касается двух других. Докажите, что точки касания их оснований лежат на одной окружности.
Решение: Представим, что каждый из конусов полый и без основания. В полученные «кульки" положим по шару так, чтобы каждый из этих шаров касался боковой поверхности своего конуса по окружности его основания. Точки касания оснований конуса будут точками касания этих четырех шаров. Проведем через три из этих точек плоскость. Используя подобие треугольников, нетрудно доказать, что четвертая точка также лежит в этой плоскости. Отсюда легко следует утверждение задачи. Задача 8: Десять волейбольных команд сыграли между собой турнир в один круг. За выигрыш давалось одно очко, за проигрыш – 0. Докажите, что если команда, занявшая i-е место, набрала xi очков, то x1 + 2x2 + ... + 10x10 ≥ 165.
Решение: Понятно, что x1 ≤ 9. Пусть x1 < 9, т.е. первая команда кому-то проиграла. Заметим, что если бы первая команда победила бы во всех своих встречах, то левая часть неравенства только уменьшилась бы. Значит, достаточно доказать неравенство только для случая x1 = 9 – а для остальных значений оно будет тем более верно. Заметим, что при x1 = 9 будет x2 ≤ 8. Аналогично рассуждая, придем к случаю x2 = 8. Далее получим: x3 = 7, x4 = 6, …x10 = 0. Однако в этом случае (который нам достаточно доказать!) неравенство выполняется. Задача 9: В США, начиная с 1950 года, издается журнал «Journal of Unclear Physics", который выпускается нерегулярно, но не реже, чем 5 номеров за три года. Докажите, что если журнал будет издаваться достаточно долго, то в некотором году его номер совпадет с номером года.
Решение: Легко видеть, что через некоторое время номер журнала станет больше года его выпуска. Пусть N – первый год с таким свойством. Тогда в этом N-м году вышел журнал с номером N + 1. Допустим, что журнал с номером N вышел когда-то раньше. Получаем противоречие с минимальностью N. Задача 10: Докажите, что при каждом целом k ≥ 0 число 26k + 1 + 36k + 1 + 56k + 1 делится на 7. Решение: Указание. Числа 26, 36 и 56 дают остаток 1 от деления на 7.
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> III, 1992 >> Турнир матбоёв >> 1-й тур | Убрать решения |