Задача 1: Существует ли многочлен P(x) такой, что для всех x выполняется неравенство P(x)P′(x) – x(P″(x))² > 0?

Решение: Докажите, что левая часть неравенства представляет собой многочлен нечетной степени (который имеет хотя бы один действительный корень), а значит, неравенство не может выполняться для всех действительных чисел.

Задача 2: Дан полукруг и прямая a, перпендикулярная его диаметру AB и удаленная на расстояние AB от точки B; к полукругу проведена касательная в точке K, пересекающая прямую a в точке M. Через точку B проведена прямая, параллельная AK, до пересечения с KM в точке N. Докажите, что произведение длин отрезков KN и MN не зависит от выбора точки K.

Решение: Докажите, что NM × KN = 2r², где r – радиус полукруга.

Задача 3: Делится ли число 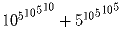на 11?

Решение: Делится, т.к. первое слагаемое дает остаток 10, а второе – остаток 1 от деления на 11.

Задача 4: За круглым столом сидят n человек, пронумерованных по порядку от 1 до n, на стульях, также пронумерованных от 1 до n, но в произвольном порядке. При каких n их всегда можно пересадить по кругу (т.е. «повернуть" относительно стульев) так, чтобы никакой номер стула, на котором сидит человек, не совпал с номером этого человека?

Решение: Ответ: при четных n.

Задача 5: Пусть S(n) – сумма цифр числа n в десятичной записи, а  σ (n) = S(1) + S(2) + ... + S(n). Докажите, что sigma(n) < 9(n +  ㏑ (n!)).

Решение: Пусть K(m) – количество цифр в числе n. Тогда 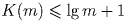. Но S(m) ≤ 9K(m). Просуммировав по всем значениям от 1 до n, получим требуемое неравенство.

Задача 6: Существует ли бесконечная последовательность из нулей и единиц, в которой никакой конечный блок не повторяется три раза подряд?

Решение: Т.к. каждое подслово длины k есть начало подслова длины k + 1, то число подслов длины k не меньше числа подслов длины k + 1; причем равенство возможно только в том случае, когда слово периодично. Если в слове встречается только одна буква, то оно уже периодично. Если же букв (т.е. подслов длины 1) больше 1, а подслов длины 1992 ровно 1992, то при некотором k число подслов длины k равно числу подслов длины k + 1, т.е. опять периодичность.

Задача 7: Докажите, что для любых десяти точек A₁,  …  ,A₁₀ единичной сферы с центром O среди треугольников A_iA_jO (1 ≤ i < j ≤ 10) найдется хотя бы один треугольник с площадью не более 0,48.

Решение: Окружим каждую из точек «шапочкой" на сфере так, чтобы угол в осевом сечении соответствующего ей конуса был равен 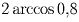. Оценив суммарную площадь шапочек, легко видеть, что среди них найдутся две перекрывающиеся. Нетрудно убедиться, что центры этих шапочек порождают искомый треугольник.

Задача 8: Две окружности пересекаются в точках A и B. AC – хорда первой окружности, касающаяся второй окружности; AD – хорда второй, касающаяся первой. Прямая CD пересекает первую окружность в точке M, отличной от точек A, B, C, D. Докажите, что прямая BM делит отрезок AD пополам.

Решение: Обозначим через N точку пересечения прямой MB со второй окружностью, отличную от точки B. Тогда ANDM – параллелограмм, т.к. четырехугольник ABMC – вписанный.

Задача 9: Многочлен x¹⁹⁹² + x¹⁹⁹¹ + x¹⁹⁹⁰ + x³ + x² + x + 1 разделили с остатком на многочлен x³ – 6x² + 11x – 6. Найдите этот остаток.

Решение: Ответ:

Задача 10: В таблице (n + 2) × (n + 2) по границе расставлены нули, а во внутреннем квадрате n × n – числа n^2. Для каждых двух соседних (имеющих общую сторону) клеток вычислим модуль разности стоящих в них чисел, а затем просуммируем полученные числа по всем парам соседних клеток. При каком расположении чисел n^2 эта сумма минимальна?

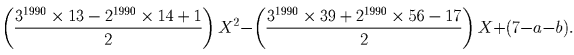
Задача 92: 2.10