 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> III, 1992 >> Турнир матбоёв >> 3-й тур | Убрать решения |
|
|
| III Всероссийский фестиваль юных математиков. Краснодар. 1992. Турнир матбоёв. 3-й тур |
|
|
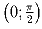 .
.Решение: Заметим, что левая часть строго возрастает, а правая – строго убывает. Значит, уравнение имеет единственное решение:
 .
Задача 2:
Докажите, что ни при каком натуральном n 5n – 1 не делится на
4n – 1.
.
Задача 2:
Докажите, что ни при каком натуральном n 5n – 1 не делится на
4n – 1.Решение: При нечетных n правая часть делится на 3, а левая – не делится. При четных n правая часть делится на 5, а левая – не делится. Задача 3: Число состоит из нулей и единиц. С ним можно делать такую операцию: любой блок «01" можно заменить на блок «1000". Докажите, что такую операцию можно проводить лишь конечное число раз.
Решение: В какой-то момент самая левая единица перестанет двигаться. После этого момента отбросим эту единицу и все, что левее нее. Теперь есть новая «самая левая" единица – когда-нибудь и она перестанет двигаться и т.д. Значит, когда-нибудь все единицы перестанут двигаться, т.е. мы больше не сможем проводить операцию. Задача 4: На плоскости дано конечное множество точек такое, что серединный перпендикуляр к любому отрезку, соединяющему какие-то две точки этого множества, проходит ровно через две точки этого множества. Докажите, что в этом множестве не меньше восьми точек.
Решение: Пусть AC – CB = m, J – центр вписанной окружности, K – точка касания ее с AB. Т.к. AK = (AB + m)/2, то положение точки K постоянно. А т.к. ∠ AJB > 90, то точка J лежит внутри отрезка DK, где D – такая точка, что ∠ ADB = 90. Ответ: два отрезка без концов – DK и симметричный ему относительно AB. Задача 5: На плоскости даны точки A и B. Рассмотрим точки C, не лежащие на прямой AB и такие, что величина AC × BC постоянна. Найдите ГМТ центров окружностей, вписанных в треугольник ABC.
Задача 6: На сторонах BC, CA и AB треугольника ABC взяты точки A1, B1, C1 соответственно так, что отрезки AA1, BB1 и CC1 пересекаются в одной точке. Пусть M – проекция точки A1 на B1C1. Докажите, что MA1 – биссектриса угла BMC.
Решение: Используйте теоремы Чевы и Менелая и понятие окружности Аполлония. Задача 7: Можно ли бумажный квадрат n × n сложить так, чтобы одним взмахом ножниц его можно было бы разрезать на n² квадратов 1 × 1?
Решение: Да, можно – это легко доказывается по индукции. Задача 8: В окружность вписан выпуклый четырехугольник, у которого одна из пар противоположных сторон по длине совпадает с парой сторон правильного шестиугольника и квадрата, вписанных в эту окружность. Меньшая диагональ этого четырехугольника делится точкой пересечения диагоналей в отношении 1:2. Одной линейкой постройте центр окружности. Задача 9: Для всех положительных a, b,c докажите неравенство: a³ + b³ + c³ + 6abc ≥ (a + b + c)³/4.
Решение: Заменив переменные, придем к: x³ + y³ + z³ + 6xyz ≥ ¼, где x + y + z = 1. Отсюда получаем 4xy(x + y) + 4xz(x + z) + 4yz(y + z) ≤ 1, что легко доказывается.
Задача 10: На плоскости дан вектор. Его разрешается проектировать на любую прямую. Можно ли его таким образом повернуть на 90, чтобы его длина изменилась меньше, чем на 1%?
Решение: Если вектор n раз повернуть (проектируя) на угол
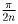 , то он повернется на угол
, то он повернется на угол  ; а его длина
при этом измениться в
; а его длина
при этом измениться в  раз. Нетрудно
доказать, что при достаточно больших n эта величина больше 0,99,
т.е. ответ: да.
раз. Нетрудно
доказать, что при достаточно больших n эта величина больше 0,99,
т.е. ответ: да.
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> III, 1992 >> Турнир матбоёв >> 3-й тур | Убрать решения |