 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> IV, 1993 >> Турнир матбоёв >> Финал | Убрать решения |
|
|
| IV Всероссийский фестиваль юных математиков. Майкоп. 1993. Турнир матбоёв. Финал |
|
|
Решение: При всех m > 2. Задача 2: На плоскости дан угол, внутри которого отмечена точка O. Проведите через O такой отрезок BC, что значение выражения максимально, если точки B и C лежат на сторонах угла или их продолжениях.
Задача 3: Существует ли натуральное число n > 10\,000\,000\,000 такое, что все простые делители числа n³ – 1 меньше n?
Решение: Возьмем n = k², где k = 1\,000\,000,000. Тогда
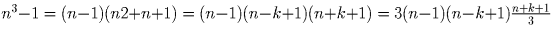 . Заметим, что n + k + 1 делится на 3, т.е. мы
представили наше число в виде произведения четырех целых
сомножителей, каждый из которых меньше n.
Задача 4:
Существует ли выпуклый 1\,000\,000\,000-угольник с вершинами,
имеющими целочисленные координаты, диаметр которого не превосходит
1\,000\,000\,000\,000?
. Заметим, что n + k + 1 делится на 3, т.е. мы
представили наше число в виде произведения четырех целых
сомножителей, каждый из которых меньше n.
Задача 4:
Существует ли выпуклый 1\,000\,000\,000-угольник с вершинами,
имеющими целочисленные координаты, диаметр которого не превосходит
1\,000\,000\,000\,000?Решение: Нет, не существует. Задача 5: Царь страны Суесловии некоторые слова объявил скверными. При этом для каждого n скверных слов длины n оказалось не более одного. Докажите, что если алфавит Суесловии состоит из пяти букв, то можно составить сколь угодно длинную речь, которая, будучи напечатанной с любой расстановкой пробелов, не содержала бы скверных слов.
Решение: Назовем слово пристойным, если оно не содержит скверных подслов. Пусть Π (n) – число пристойных слов длины ровно n. Можно доказать, что Π (n + 1) > 2 Π (n), откуда следует утверждение задачи. Задача 6: Можно ли расставить числа n в таком порядке, чтобы ни для каких двух чисел их полусумма не равнялась ни одному из чисел, поставленных между ними?
Решение: Можно. Понятно, что если мы доказали этот факт для некоторого значения n, то он верен и для всех меньших значений. Значит, достаточно доказать лишь для n = 2k . Воспользуемся методом математической индукции. База проверяется легко. Покажем теперь, как расставить числа при n = 2k + 1. Сначала выпишем все четные числа, воспользовавшись предположением индукции (т.е. все числа случая будут просто удвоены). Затем выпишем все нечетные числа «в том же порядке" (т.е. от каждого четного числа отнимем единицу – получим соответствующее нечетное число). Нетрудно убедиться, что такая запись удовлетворяет условию. Задача 7: Дан вписанный четырехугольник ABCD. E – точка пересечения его диагоналей, а A′, B′, C′, D′ – основания перпендикуляров, опущенных из E на стороны AB, BC, CD, DA соответственно. Докажите, что прямые A′B′, C′D′ и AC пересекаются в одной точке.
Задача 8: Коробка m × n заполнена прямоугольниками 1 × k. Разрешается выбрать k прямоугольников, образующих квадрат k × k, и поменять у них одновременно ориентацию. Докажите, что все прямоугольники можно сориентировать одинаково.
Задача 9: Число n называется периодическим в некоторой системе счисления, если существует число a такое, что в этой системе счисления запись n есть повторенная несколько раз запись числа a (n и a – натуральные, a ≠ 1; a называется периодом числа n). Докажите, что числа вида p², где p простое число, ни в одной системе счисления не являются периодическими.
Решение: Если число периодическое с периодом a, то оно представимо в виде a × 100 … 0100 … 100 … … … 01, где количество единиц совпадает с количеством повторений периода в числе, а «расстояние" между единицами – длина числа a. Но, значит, эти два сомножителя в представлении нашего числа различны, а значит, наше число не может быть квадратом простого. Задача 10: Назовем пару клеток квадратной доски «дружественной", если они являются крайними клетками в некотором прямоугольнике 1 × 4. Можно ли доску 100 × 100 разбить на пары «дружественных" клеток?
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> IV, 1993 >> Турнир матбоёв >> Финал | Убрать решения |