 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> IV, 1993 >> Турнир матбоёв >> 1-й тур | Убрать решения |
|
|
| IV Всероссийский фестиваль юных математиков. Майкоп. 1993. Турнир матбоёв. 1-й тур |
|
|
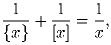
Решение: Исходное уравнение эквивалентно
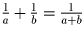 , где a и b – целая и дробная части
числа. Нетрудно убедиться, что последнее уравнение не имеет решений.
Задача 2:
Четыре окружности расположены так, что каждая касается внешним
образом двух других. Каждая из этих окружностей касается внутренним
образом пятой окружности в точках A, B, C, D. Докажите, что
AB × CD = BC × DA.
, где a и b – целая и дробная части
числа. Нетрудно убедиться, что последнее уравнение не имеет решений.
Задача 2:
Четыре окружности расположены так, что каждая касается внешним
образом двух других. Каждая из этих окружностей касается внутренним
образом пятой окружности в точках A, B, C, D. Докажите, что
AB × CD = BC × DA.Задача 3: Докажите, что если при всех целых x многочлен P(x) принимает только целые значения и для любых натуральных n и x последовательность остатков от деления на n чисел x, P(x), P(P(x)), …, P(P(...P(x))...), и т.д. периодична, то все коэффициенты многочлена P(x) – целые.
Задача 4: Шкаф прямоугольной формы можно передвигать, поворачивая вокруг одной из ножек (слегка приподнимая остальные). После какого минимального числа поворотов шкаф может оказаться на том же месте, но повернутым на 180? Решение: Заметим, что положение прямоугольного шкафа ABCD полностью описывается одной из его диагоналей AC. Легко видеть, что двух поворотов недостаточно. Покажем, как можно обойтись тремя поворотами. Построим правильный треугольник EFG, и пусть шкаф стоит ножками A и C соответственно в точках E и F. Первым поворотом – относительно точки E – передвинем C в G. Вторым поворотом – относительно G – передвинем A в F. Наконец, последним поворотом – относительно новой F – передвинем C в E. Задача 5: Существует ли функция, непрерывная на вещественной оси и принимающая каждое свое значение ровно два раза?
Решение: Пусть какое-то значение – допустим, значение 0 – функция принимает в точках a и b. Так как больше нулей у нее нет, то на всем интервале (a,b) функция либо положительна, либо отрицательна – пусть положительна. Рассмотрите максимальное значение, принимаемое функцией на отрезке [a,b]. Задача 6: На плоскости отмечены 6 точек, никакие три из которых не лежат на одной прямой и все попарные расстояния между которыми различны. Докажите, что среди всех треугольников с вершинами в этих точках найдутся два треугольника с общей стороной такой, что для одного из них эта сторона является наибольшей, а для другого – наименьшей.
Задача 7: Дан остроугольный треугольник ABC. Найдите геометрическое место точек M таких, что ∠ MAB = ∠ MCB, ∠ MBA = ∠ MCA.
Решение: Ответ: описанная около треугольника окружность и его ортоцентр. Задача 8: В кубиках, составляющих куб n × n × n, написаны действительные числа так, что сумма чисел в каждом кубике 2 × 2 × 2 равна 10. При каких n можно утверждать, что сумма чисел в восьми угловых кубиках также равняется 10?
Задача 9: Решите в натуральных числах уравнение: 7n = 6n + m².
Решение: Если n четно, то 7n – 6n дает остаток 6 от деления на 7, т.е. не может быть полным квадратом. Если же n нечетно и больше единицы, то 7n – 6n дает остаток 3 от деления на 4 и опять не может быть полным квадратом. Единственное решение: n = m = 1. Задача 10: Можно ли в пространстве выбрать 1993 отрезка так, чтобы любая плоскость пересекала не более трех из них?
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> IV, 1993 >> Турнир матбоёв >> 1-й тур | Убрать решения |