 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> V, 1994 >> Турнир матбоёв >> Первая лига >> 4-й тур | Убрать решения |
|
|
| V Всероссийский фестиваль юных математиков. Михайловский. 1994. Турнир матбоёв. Первая лига. 4-й тур |
|
|
Решение: Отбросив одну монету, которая точно настоящая, получим известную задачу: 13 монет, из которых одна фальшивая. Задача 2: Задача 3: Докажите, что число 25¹º¹ + 37¹º¹ не делится нацело на 1994.
Задача 4: Шахматная фигура «гроссшпрингер" ходит так: на p клеток в одном направлении (по горизонтали или вертикали) и на q в перпендикулярном. Найдите все p и q, для которых гроссшпрингер из любой клетки бесконечной шахматной доски может попасть в любую другую клетку.
Задача 5: Существует ли функция f(x):R → R, которая для любого x удовлетворяет условию f(f(x)) = sin x?
Задача 6: Найдите наименьшее натуральное число, кратное 5, сумма цифр которого равна 24.
Решение: Ответ: 1995. Задача 7: Дан параллелограмм ABCD. На сторонах BC и CD и диагонали BD взяты соответственно точки N, K и M так, что прямая MN параллельна AB, а прямая MK параллельна AD. Отрезки AN и AK пересекают диагональ BD в точках E и F соответственно. Докажите, что площадь треугольника AEF равна сумме площадей треугольников BEN и FKD.
Решение: Площади треугольников AMK и MDK равны, значит, площади треугольников AMF и FKD тоже равны. Аналогично, равны площади треугольников AEM и BEN. Задача 8: На клетчатой бумаге в квадрате 2n × 2n (с границами) строится несамопересекающаяся (т.е. без общих точек) ломаная с единичными звеньями, проходящая по линиям сетки, причем каждые два соседних звена перпендикулярны. Какую наибольшую длину может иметь такая ломаная?
Задача 9: Решите систему уравнений:
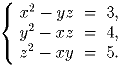
Решение: Вычтем из второго уравнения первое: (y – x)(x + y + z) = 1; вычтем из третьего уравнения второе: (z – y)(x + y + z) = 1. Значит, 2y = x + z. Подставив выраженный отсюда y во второе уравнение, получим (x – z)² = 16. Теперь уже нетрудно, рассмотрев два случая, получить ответ: (11/6, – 1/6, – 13/6) и ( – 11/6,1/6,13/6). Задача 10: Дан острый угол BAC и замкнутая ломаная AA1A2...AnA, длины всех звеньев которой равны. Найдите величину угла BAC, если точки A1, A3, A5,…все различны и лежат на луче AB, а точки A2, A4, A6, … все различны и лежат на луче AC.
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> V, 1994 >> Турнир матбоёв >> Первая лига >> 4-й тур | Убрать решения |