 |
 |
|
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> V, 1994 >> Турнир матбоёв >> Высшая лига >> 3-й тур | Убрать решения |
|
|
| V Всероссийский фестиваль юных математиков. Михайловский. 1994. Турнир матбоёв. Высшая лига. 3-й тур |
|
|
Решение: Раскрыв скобки, получаем: x4 + y4 + x²y² ≤ x³y + xy³ + 1. Без ограничения общности можно считать, что x ≥ y. Но тогда xy³ ≥ y4, x³y ≥ x²y², а 1 ≥ x4.
Задача 2: Дан параллелограмм ABCD ( ∠ BAD – острый). Биссектриса угла BAD пересекает сторону CD в точке L, а прямую BC – в точке K. Пусть O – центр окружности, описанной около треугольника LCK. Докажите, что точки D, B, C и O лежат на одной окружности.
Задача 3: Дана функция f(x) = x² – 3|x| + 4. Найдите все множества A, состоящие из конечного числа элементов и обладающие следующим свойством: для любого числа x, принадлежащего множеству A, число f(x) также принадлежит множеству A.
Решение: Заметим, что если x > 2, то f(x) > x, но т.к. A – конечное множество, то таких чисел в нем нет. Аналогично, если 0 ≤ x < 1, то f(x) > 2, и таких чисел тоже нет. Кроме того, если 1 < x < 2, то 1 < f(x) < 2 и f(x) > x, значит, таких чисел тоже нет. Т.к. f(x) – четная функция, то все вышесказанное относится и к соответствующим отрицательным числам. Перебирая оставшийся набор чисел, получаем ответ: 2, 1,2, – 2,2, – 1,2, – 2, – 1,2, – 2,1,2, – 1,1,2, – 2, – 1,1,2. Задача 4: Можно ли разбить множество натуральных чисел на три непустых попарно непересекающихся множества так, чтобы для каждой пары чисел x и y, взятых из любых двух разных множеств, число xy + x + y принадлежало бы третьему множеству?
Решение: Обозначим f(x,y) = xy + x + y. Заметим, что f(1,5) = f(2,3) = 11. Значит, либо 1 и 3 в первой группе, а 2 и 5 – во второй, либо 1 и 2 – в первой, а 3 и 5 – во второй. Первый случай не подходит, т.к. f(2,1) = 5. Во втором случае получаем, что f(1,3) = 7 вместе с 11 – в третьей группе, но тогда f(1,7) = 15 – во второй, и получаем противоречие из f(15,1) = f(7,3). Задача 5: Даны последовательности an и dn: an = 100 + n², dn – наибольший общий делитель чисел an и an + 1. Какое наибольшее значение может принимать dn?
Задача 6: Найдите все функции f(x):R → R, которые для любых x и y удовлетворяют равенству f(x² + y) = f(x) + f(y).
Решение: Подставив x = y = 0, получаем f(0) = 0. Подставив y = 0, получаем f(x²) = f(x), откуда f(x) = f( – x), т.е. функция нечетна. Подставив y = – x², получим f(x) = – f( – x²). Итак, f( – x²) = f(x²) = f(x) = – f( – x²), откуда, используя нечетность, получаем, что наша функция – тождественный нуль. Задача 7: Даны 27 (не обязательно различных) положительных чисел
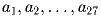 . Рассматриваются тройки индексов (k,m,n) такие, что
ak < am, ak + am = an. Каково наибольшее возможное количество
таких троек?
. Рассматриваются тройки индексов (k,m,n) такие, что
ak < am, ak + am = an. Каково наибольшее возможное количество
таких троек?Задача 8: Сфера с центром O касается всех ребер тетраэдра. Четыре сферы с центрами в вершинах тетраэдра попарно касаются друг друга внешним образом, а также касаются некоторой сферы с центром O. Докажите, что тетраэдр является правильным.
Задача 9: Пусть α (x) и β (x) – многочлены, степень каждого из которых больше единицы, ρ (x) = α ( β (x)). Пусть многочлен ρ (x) – четен. Докажите, что многочлен β (x) – β (0) – четен или нечетен.
Задача 10: В стране 22 аэродрома, и каждый связан авиарейсами с тремя другими. Докажите, что есть такая пара аэродромов A и B, для которой любой перелет из A в B требует не менее трех пересадок.
Решение: Предположим противное. Зафиксируем какой-то город A. Обозначим через Sn множество городов, в которые можно добраться из A за n перелетов и нельзя быстрее. Тогда в S1 три города, в S2 шесть городов, а в S3 12 городов – всего 1 + 3 + 6 + 12 = 22 города. Выберем в S3 какой-нибудь город B. Небольшим перебором убеждаемся, что в S3 есть город C, в который нельзя добраться из B за три перелета.
| Задачная база >> Соревнования всероссийского уровня >> Всероссийский фестиваль юных математиков >> V, 1994 >> Турнир матбоёв >> Высшая лига >> 3-й тур | Убрать решения |