Задача 1: Выпуклый многоугольник составлен из n > 1 равных (возможно, перекрывающихся) равносторонних треугольников так, что стороны всех треугольников попарно непараллельны. Каково наименьшее возможное значение n?

Решение: Ответ: 5.

Задача 2: На плоскости даны окружность и точка A вне нее. Рассматриваются всевозможные треугольники ABC, описанные около данной окружности. Найдите геометрическое место точек пересечения биссектрисы угла B со средней линией (или ее продолжением) треугольника ABC, параллельной стороне BC.

Задача 3: Решите систему уравнений в действительных числах:

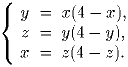
Задача 4: Сумма квадратов двух натуральных чисел делится на простое число p вида 4n – 1 (n ∈ N). Докажите, что каждое из них делится нацело на p.

Задача 5: Докажите, что при всех a,b,c ∈ [1;2] выполняется неравенство:

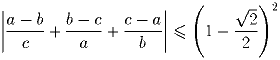
Задача 6: Через точку M, лежащую внутри окружности, проведены 4 различных хорды A_kB_k, где k = 1,2,3,4. Докажите, что точка P пересечения прямых A₁A₂ и A₃A₄, точка Q пересечения прямых B₁B₂ и B₃B₄, а также точка M лежат на одной прямой.

Задача 7: Дано натуральное число k. При каких m и n прямоугольник m × n (m,n > k²) можно разрезать на квадраты, сторона каждого из которых равна k или k + 1?

Задача 8: Найдите сумму модулей всех различных корней уравнения

Задача 9: При каком наибольшем натуральном n число n! представляется в виде произведения n – 3 последовательных натуральных чисел?

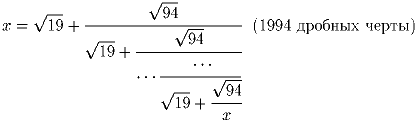
Решение: Пусть 1 × 2 ×  …  × n = (k + 1) × (k + 2) ×  …  × (k + n – 3). После преобразований получаем: 1 × 2 ×  …  × k = (n + 1) × (n + 2) ×  …  × (k + n – 3). При n = 23 и k = 4 это равенство выполняется. Пусть n ≥ 24. При k = 4 левая часть равна 4! = 24, а правая – n + 1 ≥ 25. При дальнейшем увеличении k правая часть будет возрастать быстрее левой. Значит, ответ: 23.

Задача 10: Связный граф содержит конечное число вершин и ребер, причем ребра покрашены в два цвета: красный и синий. За один ход можно перекрасить все ребра, выходящие из одной вершины. Все возможные раскраски ребер этого графа разбиваются на несколько классов таких, что раскраски из одного класса можно получить друг из друга за несколько ходов, а из разных – нельзя. Докажите, что число таких классов равняется количеству раскрасок, в которых из каждой вершины выходит четное число красных ребер.